
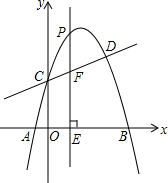
 如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.分析 (1)首先求出点C的坐标,然后利用待定系数法求出一次函数和抛物线的解析式;
(2)本问采用数形结合的数学思想求解.将直线y=$\frac{1}{2}$x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;
(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.
解答 解:(1)∵直线y=kx+2经过点C,D,
∴$C(0,2),\frac{7}{2}=3k+2$,
∴$k=\frac{1}{2}$,
∴直线CD的解析式为$y=\frac{1}{2}x+2$,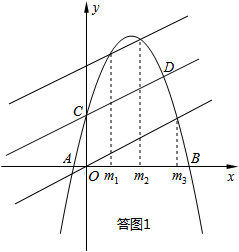
∵抛物线$y=a{x^2}+\frac{7}{2}x+c$经过点C,D,
∴$\left\{\begin{array}{l}2=c\\ \frac{7}{2}=9a+\frac{21}{2}+c\end{array}\right.\;\;\;\;\;\;\;\;\;\;∴\left\{\begin{array}{l}a=-1\\ c=2\end{array}\right.$,
∴抛物线的解析式为$y=-{x^2}+\frac{7}{2}x+2$;
(2)如图1,
∵点P的横坐标为m且在抛物线上,
∴$P(m,-{m^2}+\frac{7}{2}m+2),F(m,\frac{1}{2}m+2)$,
∵PF∥CO,
∴当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形,
①当0<m<3时,$PF=-{m^2}+\frac{7}{2}m+2-(\frac{1}{2}m+2)=-{m^2}+3m$,
∴-m2+3m=2,解得:m1=1,m2=2,
即当m=1或2时,四边形OCPF是平行四边形,
②当m≥3时,$PF=(\frac{1}{2}m+2)-(-{m^2}+\frac{7}{2}m+2)={m^2}-3m$m2-3m=2,
解得:${m_1}=\frac{{3+\sqrt{17}}}{2},{m_2}=\frac{{3-\sqrt{17}}}{2}$(舍去),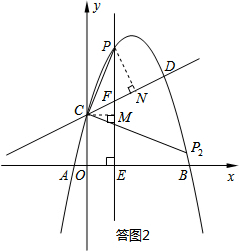
即当${m_1}=\frac{{3+\sqrt{17}}}{2}$时,四边形OCFP是平行四边形;
(3)如图2,当点P在CD上方且∠PCF=45°时,
作PN⊥CD,CM⊥PE,则△PMF∽△CNF,
∴$\frac{PM}{MF}=\frac{CN}{FN}=\frac{m}{{\frac{1}{2}m}}=2$,
∴PM=CM=2CF,
∴$PF=\sqrt{5}FM=\sqrt{5}CF=\sqrt{5}×\frac{{\sqrt{5}}}{2}CN=\frac{5}{2}CN=\frac{5}{2}m$,
又∵PF=-m2+3m,
∴$-{m^2}+3m=\frac{5}{2}m$,
解得:${m_1}=\frac{1}{2}$,m2=0(舍去)
∴$P(\frac{1}{2},\frac{7}{2})$.
同理可以求得:另外一点为$P(\frac{23}{6},\frac{13}{18})$.
∴符合条件的点P的坐标为($\frac{1}{2}$,$\frac{7}{2}$)或($\frac{23}{6}$,$\frac{13}{18}$).
点评 本题是二次函数综合题型,考查了二次函数的图象与性质、一次函数的图象与性质、解方程(方程组)、平行四边形、相似三角形(或三角函数)、勾股定理等重要知识点.第(2)问采用数形结合思想求解,直观形象且易于理解;第(3)问中,符合条件的点P有两个,注意不要漏解.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x+1}$ | B. | $\sqrt{x-1}$ | C. | $\sqrt{x}$+1 | D. | $\sqrt{x}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
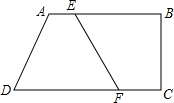 如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则3秒时四边形ADFE是平行四边形.
如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则3秒时四边形ADFE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
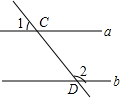 如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )| A. | 135° | B. | 145° | C. | 155° | D. | 165° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
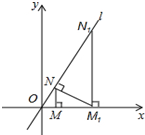 如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).
如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com