
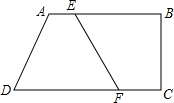
 如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则3秒时四边形ADFE是平行四边形.
如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则3秒时四边形ADFE是平行四边形.  名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:选择题
 不等式组的解集在数轴上表示如图,则该不等式组是( )
不等式组的解集在数轴上表示如图,则该不等式组是( )| A. | $\left\{\begin{array}{l}x≥-1\\ x≤2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<-1\\ x≥2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>-1\\ x<2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>-1\\ x≤2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
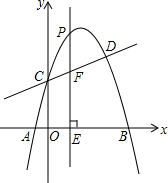 如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
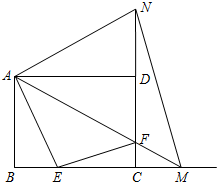 如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B、C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C、D)以每秒1个单位长度的速度,匀速向点D运动;点E、F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD延长线于点N,连接MN.设运动时间为t秒.
如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B、C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C、D)以每秒1个单位长度的速度,匀速向点D运动;点E、F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD延长线于点N,连接MN.设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
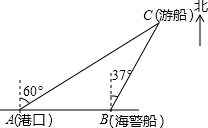 一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向.
一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=56}\\{2×16x=24y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=56}\\{2×24x=26y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=56}\\{16x=24y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=56}\\{24x=16y}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com