
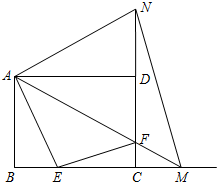
 如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B、C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C、D)以每秒1个单位长度的速度,匀速向点D运动;点E、F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD延长线于点N,连接MN.设运动时间为t秒.
如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B、C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C、D)以每秒1个单位长度的速度,匀速向点D运动;点E、F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD延长线于点N,连接MN.设运动时间为t秒.分析 (1)根据相似三角形的对应边成比例,列出关于t的式子,求出t;
(2)证明△ABE∽△ADN,得到成比例线段,用t表示BE、CF、DN,代入比例式求出t的值;
(3)根据△AMN的面积=△ANF的面积+△MNF的面积,求出△AMN的面积,可知是否是定值.
解答 解:(1)若△ABE∽△ECF,
则$\frac{BE}{AB}$=$\frac{CF}{EC}$,
∴$\frac{2t}{9}$=$\frac{t}{12-2t}$,
解得t1=0(舍去),t2=$\frac{15}{4}$,
∴当t=$\frac{15}{4}$时,△ABE∽△ECF;
(2)存在,
在矩形ABCD中,∠B=∠BAD=∠ADC=∠ADN=90°,
又∵AE⊥AN
∴∠NAE=90°,
∴∠BAE=∠DAN,
∴△ABE∽△ADN,
∴$\frac{BE}{AB}$=$\frac{DN}{AD}$,
∵AB=9,BE=2t,AD=12,CF=t,
∴DF=9-t,
由折叠知:DN=DF=9-t,
∴$\frac{2t}{9}$=$\frac{9-t}{12}$,
∴t=$\frac{27}{11}$,
∴当t=$\frac{27}{11}$时,AE⊥AN,
(3)△AMN的面积不变,
在矩形ABCD中,FC∥AB,
∴△FCM∽△ABM
∴$\frac{FC}{AB}$=$\frac{MC}{BM}$,
∴$\frac{t}{9}$=$\frac{MC}{12+MC}$,
∴MC=$\frac{12t}{9-t}$,
∴S△AMN=S△ANF+S△NFM
=$\frac{1}{2}$NF×AD+$\frac{1}{2}$NF×MC
=$\frac{1}{2}$NF(AD+MC)
=$\frac{1}{2}$×2(9-t)×(12+$\frac{12t}{9-t}$)
=108.
∴△AMN的面积不变为108.
点评 本题考查的是相似三角形的综合应用,灵活运用相似三角形的判定定理和性质定理是解题的关键,解答时,注意方程思想的正确运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 菱形的对角线互相平分且相等 | |
| B. | 矩形的对角线互相垂直平分 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0)、B(3,0).C(2,3)三点,且与y轴交于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0)、B(3,0).C(2,3)三点,且与y轴交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
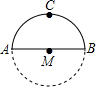 如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )
如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )| A. | 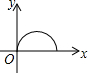 | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
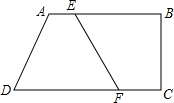 如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则3秒时四边形ADFE是平行四边形.
如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则3秒时四边形ADFE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
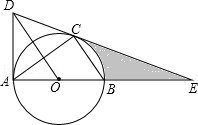 如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
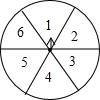 如图,是可以自由转动的转盘,该转盘被分成6个相等的扇形区域.
如图,是可以自由转动的转盘,该转盘被分成6个相等的扇形区域.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com