
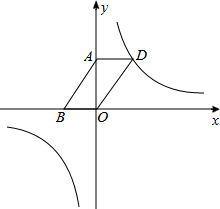
 已知反比例函数$y=\frac{m-1}{x}$(m为常数)的图象在第一、三象限内.
已知反比例函数$y=\frac{m-1}{x}$(m为常数)的图象在第一、三象限内.分析 (1)由图象在第一象限可得到关于m的不等式,可求得m的取值范围;
(2)①由平行四边形的性质可求的D点坐标,代入可求得反比例函数解析式;②以O为圆心,OD为半径作圆,再根据对称性可求得该圆与反比例函数图象的交点坐标.
解答 解:
(1)∵反比例函数$y=\frac{m-1}{x}$(m为常数)的图象在第一、三象限内,
∴m-1>0,
解得m>1;
(2)①∵四边形ABOC为平行四边形,
∴AD∥OB,AD=OB=2,
又A点坐标为(0,3),
∴D点坐标为(2,3),
∴m-1=2×3=6,
∴反比例函数解析式为$y=\frac{6}{x}$;
②如图所示,以O为圆心,OD长为半径作圆O,与双曲线$y=\frac{6}{x}$分别交于D,P1,P2,P3四点.
根据图形的对称性,得
点D(2,3)关于直线y=x对称点P1的坐标为(3,2);
点D(2,3)关于原点中心对称点P2的坐标为(-2,-3);
点P1(3,2)关于原点中心对称点$P_3^{\;}$的坐标为(-3,-2).
由于O、D、P2三点共线.
所以符合题意的P点只有两点,其坐标分别为(3,2),(-3,-2).
点评 本题主要考查反比例函数的综合应用,涉及知识点有反比例函数的图象与性质、待定系数法求函数解析式、等腰三角形的性质等.在(1)中注意反比例函数y=$\frac{k}{x}$(k≠0)中k与图象的关系,在(2)①中求得D点坐标是解题的关键,在②中确定出P点的位置是解题的关键.本题主要考查基础知识,难度不大.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
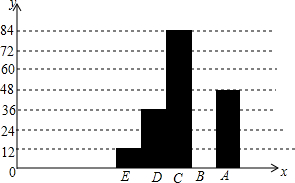 为了解某县九年级学生中考体育成绩,现从中随机抽取部分学生的体育成绩进行分段(E:0≤x<13;D:13≤x<19;C:19≤x<24;B:24≤x<30;A:30分》)
为了解某县九年级学生中考体育成绩,现从中随机抽取部分学生的体育成绩进行分段(E:0≤x<13;D:13≤x<19;C:19≤x<24;B:24≤x<30;A:30分》)| 中考体育成绩(分段)统计表 | ||
| 分数段 | 人数(人) | 频率 |
| A | 48 | 0.20 |
| B | a | 0.25 |
| C | 84 | 0.35 |
| D | 36 | b |
| E | 12 | 0.05 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
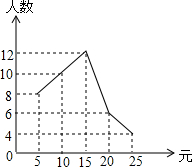 某班40名学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中40个捐款额的中位数是15元.
某班40名学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中40个捐款额的中位数是15元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com