
 如图,⊙O的直径为16,AB、CD是互相垂直的两条直径,点P是弧AD上任意一点,经过P作PM⊥AB于M,PN⊥CD于N,点Q是MN的中点,当点P沿着弧AD从点A移动到终点D时,点Q走过的路径长为2π.
如图,⊙O的直径为16,AB、CD是互相垂直的两条直径,点P是弧AD上任意一点,经过P作PM⊥AB于M,PN⊥CD于N,点Q是MN的中点,当点P沿着弧AD从点A移动到终点D时,点Q走过的路径长为2π. 科目:初中数学 来源: 题型:解答题
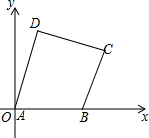 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)
如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点.
如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两条公路0A和0B相交于点0,在∠A0B的内部有工厂C和D.现要修建一个货站P到两条公路0A、0B的距离相等,且到两工厂C、D的距离相等.用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路0A和0B相交于点0,在∠A0B的内部有工厂C和D.现要修建一个货站P到两条公路0A、0B的距离相等,且到两工厂C、D的距离相等.用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的平面直角坐标系中,描出下列各点,再依次连接各点,构成封闭图形,A(-4,3),B(4,3),C(4,-3),D(-4,-3).回答下列问题:
在如图所示的平面直角坐标系中,描出下列各点,再依次连接各点,构成封闭图形,A(-4,3),B(4,3),C(4,-3),D(-4,-3).回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
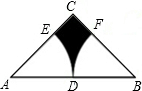 如图,Rt△ABC中,∠C=90°,AC=BC=4,点D是线段AB的中点,分别以点A,B为圆心,AD为半径画弧,分别交AC,BC于点E,F.则阴影部分面积为8-2π(结果保留π).
如图,Rt△ABC中,∠C=90°,AC=BC=4,点D是线段AB的中点,分别以点A,B为圆心,AD为半径画弧,分别交AC,BC于点E,F.则阴影部分面积为8-2π(结果保留π).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com