
【题目】如图,在![]() 中,
中,![]() ,点D.E分别是边AB、BC的中点,过点A作
,点D.E分别是边AB、BC的中点,过点A作![]() 交ED的延长线于点F,连接BF。
交ED的延长线于点F,连接BF。
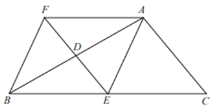
(1)求证:四边形ACEF是菱形;
(2)若四边形AEBF也是菱形,直接写出线段AB与线段AC的关系。
科目:初中数学 来源: 题型:
【题目】小明玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小明把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域内的数字(若指针在分格线上,则重转一次,直到指针指向某一区域内为止).
(1)请用列表法或画树形图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积为负数的概率.
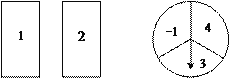
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() 。
。
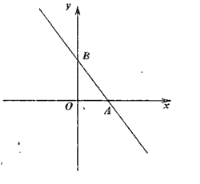
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 求点
求点![]() 的坐标。
的坐标。
(3)在![]() 轴是否存在点
轴是否存在点![]() ,使三角形
,使三角形![]() 是等腰三角形,若存在。请求出点
是等腰三角形,若存在。请求出点![]() 坐标,若不存在,请说明理由。
坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
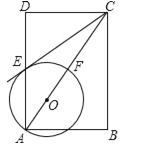
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第24个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,某校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为七年级两个班级订购了一批新的图书.七年级两个班级订购图书的情况如下表:

四大名著/套 | 老舍文集/套 | 总费用/元 | |
七年级(1)班 | 2 | 4 | 460 |
七年级(2)班 | 3 | 2 | 530 |
(1)求四大名著和老舍文集每套各是多少元?
(2)学校准备再购买四大名著和老舍文集共10套,总费用不超过800元,求学校最多能买几套四大名著?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用“<”,“>”,“=”填空:![]()
![]()
![]()
(2)由上可知:①|1﹣![]() |= ;
|= ;
②|![]() ﹣
﹣![]() |= ;
|= ;
(3)计算:|1﹣![]() |+|
|+|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |+…+|
|+…+|![]() ﹣
﹣![]() |(结果保留根号)
|(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,O,B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC,
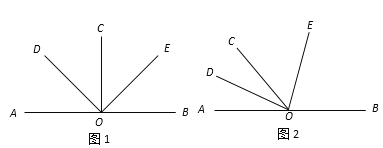
(1)若∠AOC=90°,如图1,则∠DOE= °;
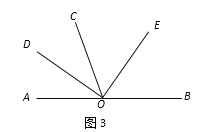
(2)若∠AOC=50°,如图2,求∠DOE的度数;
(3)由上面的计算,你认为∠DOE= °;
(4)若∠AOC=α,(0°< α <180°)如图3,求∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com