
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() 。
。
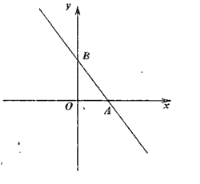
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 求点
求点![]() 的坐标。
的坐标。
(3)在![]() 轴是否存在点
轴是否存在点![]() ,使三角形
,使三角形![]() 是等腰三角形,若存在。请求出点
是等腰三角形,若存在。请求出点![]() 坐标,若不存在,请说明理由。
坐标,若不存在,请说明理由。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)在
;(3)在![]() 轴上存在点
轴上存在点![]()
![]()
![]() 使
使![]() 为等腰三角形
为等腰三角形
【解析】
(1)分别代入y=0,x=0,求出与之对应的x,y值,进而可得出点A,B的坐标;
(2)由三角形的面积公式结合S△BOP=![]() S△AOB,可得出OP=
S△AOB,可得出OP=![]() OA,进而可得出点P的坐标;
OA,进而可得出点P的坐标;
(3)由OA,OB的长可求出AB的长,分AB=AM,BA=BM,MA=MB三种情况,利用等腰三角形的性质可求出点M的坐标.
解:(1)当y=0时,-2x+4=0,解得:x=2,
∴点A的坐标为(2,0);
当x=0时,y=-2x+4=4,
∴点B的坐标为(0,4).
(2))∵点P在x轴上,且S△BOP=![]() S△AOB,
S△AOB,
∴OP=![]() OA=1,
OA=1,
∴点P的坐标为(-1,0)或(1,0).
(3))∵OB=4,OA=2,
∴AB= ![]()
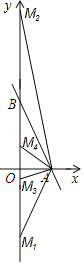
分三种情况考虑(如图所示):
①当AB=AM时,OM=OB=4,
∴点M1的坐标为(0,-4);
②当BA=BM时,BM=2![]() ,
,
∴点M2的坐标为(0,4+2![]() ),点M3的坐标为(0,4-2
),点M3的坐标为(0,4-2![]() );
);
③当MA=MB时,设OM=a,则BM=AM=4-a,
∴AM2=OM2+OA2,即(4-a)2=a2+22,
∴a=![]() ,
,
∴点M4的坐标为(0,![]() ).
).
综上所述:在y轴上存在点M,使三角形MAB是等腰三角形,点M坐标为(0,-4),(0,4+2![]() ),(0,4-2
),(0,4-2![]() )和(0,
)和(0,![]() ).
).


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】甲同学在拼图探索活动中发现,用4个形状大小完全相同的直角三角形(直角边长分别为a,b,斜边长为c),可以拼成像如图1那样的正方形,并由此得出了关于a2,b2,c2的一个等式.
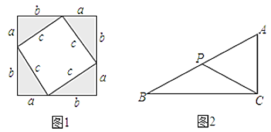
(1)请你写出这一结论:______,并给出验证过程.
(2)试用上述结论解决问题:如图2,P是Rt△ABC斜边AB上的一个动点,已知AC=5,AB=13,求PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)a5·(﹣a)3﹣(﹣2a2)4;
(2)[(x﹣2y)3]3÷[(2y﹣x)2]3
(3)﹣14﹣0.510×211+(![]() )0+3÷32
)0+3÷32
(4)(![]() )﹣1+50+[2﹣(﹣3)2]
)﹣1+50+[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.去年当地每月的平均气温如图1,小明家去年月用电量如图2.
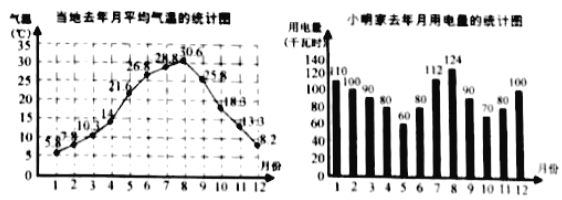
根据统计图,回答下面的问题:
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
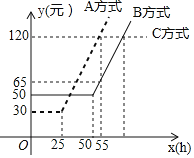
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
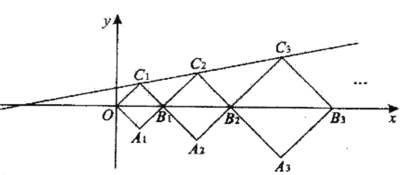
【题目】如图,在平面直角坐标系中,正方形OA1B1C1,B1A2B2C2,B2A3B3C3,···的顶点B1,B2,B3,···在x轴上,顶点C1,C2,C3···在直线y=kx+b上,若正方形OA1B1C1,B1A2B2C2的对角线OB1=2,B1B2=3, 则点C5的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D.E分别是边AB、BC的中点,过点A作
,点D.E分别是边AB、BC的中点,过点A作![]() 交ED的延长线于点F,连接BF。
交ED的延长线于点F,连接BF。
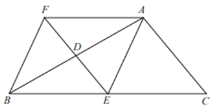
(1)求证:四边形ACEF是菱形;
(2)若四边形AEBF也是菱形,直接写出线段AB与线段AC的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
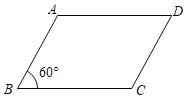
【题目】过某矩形的两个相对的顶点作平行线,再沿着平行线剪下两个直角三角形,剩余的图形为如图所示的ABCD,AB=4,BC=6,∠ABC=60°,则原来矩形的面积是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com