
【题目】甲同学在拼图探索活动中发现,用4个形状大小完全相同的直角三角形(直角边长分别为a,b,斜边长为c),可以拼成像如图1那样的正方形,并由此得出了关于a2,b2,c2的一个等式.
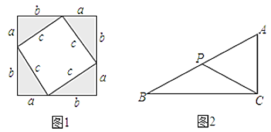
(1)请你写出这一结论:______,并给出验证过程.
(2)试用上述结论解决问题:如图2,P是Rt△ABC斜边AB上的一个动点,已知AC=5,AB=13,求PC的最小值.
【答案】(1) a2+b2=c2;(2)PC的最小值为![]() .
.
【解析】
(1)结论:a2+b2=c2,根据三角形、矩形、正方形的面积公式求解即可;
(2)根据勾股定理求出BC的长,当CP⊥AB时,PC最短,即可求出PC的最小值.
(1)结论:a2+b2=c2.
验证:∵四个三角形的面积=4×![]() =2ab,
=2ab,
四个三角形的面积=边长为![]() 的正方形面积-边长为
的正方形面积-边长为![]() 的正方形面积=(a+b)2-c2,
的正方形面积=(a+b)2-c2,
∴(a+b)2-c2=2ab,
即a2+b2=c2.
(2)∵Rt△ABC中,AC=5,AB=13,
∴52+BC2=132,
解得BC=12,
当CP⊥AB时,PC最短,
此时,![]() BC×AC=
BC×AC=![]() AB×PC,
AB×PC,
即PC=![]() =
=![]() ,
,
∴PC的最小值为![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
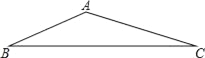
A. 450a元 B. 225a元 C. 150a元 D. 300a元
查看答案和解析>>
科目:初中数学 来源: 题型:
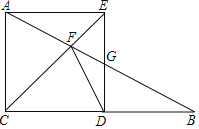
【题目】在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)(-2a3)23a3+6a12÷(-2a3);
(3)(x+1)(x-2)-(x-2)2;
(4)(a+2b+3)(a+2b-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
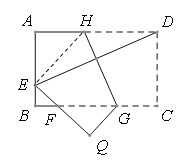
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小明把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域内的数字(若指针在分格线上,则重转一次,直到指针指向某一区域内为止).
(1)请用列表法或画树形图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积为负数的概率.
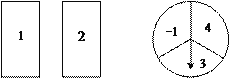
查看答案和解析>>
科目:初中数学 来源: 题型:
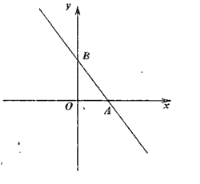
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() 。
。
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 求点
求点![]() 的坐标。
的坐标。
(3)在![]() 轴是否存在点
轴是否存在点![]() ,使三角形
,使三角形![]() 是等腰三角形,若存在。请求出点
是等腰三角形,若存在。请求出点![]() 坐标,若不存在,请说明理由。
坐标,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com