
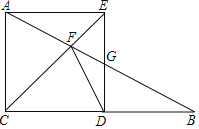
【题目】在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
【答案】(1)①FG =2![]() ;②BC=12
;②BC=12![]() ;(2)等腰三角形△DFG的腰长为4或20或
;(2)等腰三角形△DFG的腰长为4或20或![]() 或
或![]() .
.
【解析】(1)①只要证明△ACF∽△GEF,推出![]() ,即可解决问题;②如图1中,想办法证明∠1=∠2=30°即可解决问题;
,即可解决问题;②如图1中,想办法证明∠1=∠2=30°即可解决问题;
(2)分四种情形:①如图2中,当点D中线段BC上时,此时只有GF=GD,②如图3中,当点D中线段BC的延长线上,且直线AB,CE的交点中AE上方时,此时只有GF=DG,
③如图4中,当点D在线段BC的延长线上,且直线AB,EC的交点中BD下方时,此时只有DF=DG,如图5中,当点D中线段CB的延长线上时,此时只有DF=DG,分别求解即可解决问题;
(1)①在正方形ACDE中,DG=GE=6,
中Rt△AEG中,AG=![]() ,
,
∵EG∥AC,
∴△ACF∽△GEF,
∴![]() ,
,
∴![]() ,
,
∴FG=![]() AG=2
AG=2![]() .
.
②如图1中,正方形ACDE中,AE=ED,∠AEF=∠DEF=45°,
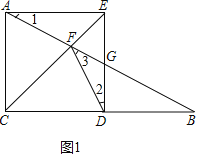
∵EF=EF,
∴△AEF≌△DEF,
∴∠1=∠2,设∠1=∠2=x,
∵AE∥BC,
∴∠B=∠1=x,
∵GF=GD,
∴∠3=∠2=x,
在△DBF中,∠3+∠FDB+∠B=180°,
∴x+(x+90°)+x=180°,
解得x=30°,
∴∠B=30°,
∴在Rt△ABC中,BC=![]() .
.
(2)在Rt△ABC中,AB=![]() =15,
=15,
如图2中,当点D中线段BC上时,此时只有GF=GD,
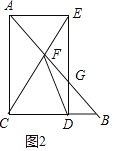
∵DG∥AC,
∴△BDG∽△BCA,
设BD=3x,则DG=4x,BG=5x,
∴GF=GD=4x,则AF=15-9x,
∵AE∥CB,
∴△AEF∽△BCF,
∴![]() ,
,
∴![]() ,
,
整理得:x2-6x+5=0,
解得x=1或5(舍弃)
∴腰长GD为=4x=4.
如图3中,当点D中线段BC的延长线上,且直线AB,CE的交点中AE上方时,此时只有GF=DG,
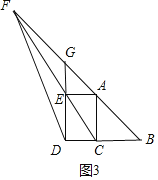
设AE=3x,则EG=4x,AG=5x,
∴FG=DG=12+4x,
∵AE∥BC,
∴△AEF∽△BCF,
∴![]() ,
,
∴![]() ,
,
解得x=2或-2(舍弃),
∴腰长DG=4x+12=20.
如图4中,当点D在线段BC的延长线上,且直线AB,EC的交点中BD下方时,此时只有DF=DG,过点D作DH⊥FG.
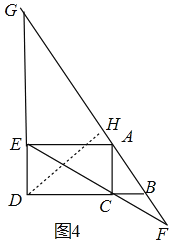
设AE=3x,则EG=4x,AG=5x,DG=4x+12,
∴FH=GH=DGcos∠DGB=(4x+12)×=
![]() ,
,
∴GF=2GH=![]() ,
,
∴AF=GF-AG=![]() ,
,
∵AC∥DG,
∴△ACF∽△GEF,
∴![]()
∴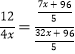 ,
,
解得x=![]() 或-
或-![]() (舍弃),
(舍弃),
∴腰长GD=4x+12=![]() ,
,
如图5中,当点D中线段CB的延长线上时,此时只有DF=DG,作DH⊥AG于H.
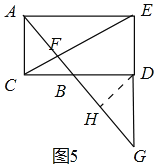
设AE=3x,则EG=4x,AG=5x,DG=4x-12,
∴FH=GH=DGcos∠DGB=![]() ,
,
∴FG=2FH=![]() ,
,
∴AF=AG-FG=![]() ,
,
∵AC∥EG,
∴△ACF∽△GEF,
∴![]() ,
,
∴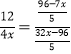 ,解得x=
,解得x=![]() 或-
或-![]() (舍弃),
(舍弃),
∴腰长DG=4x-12=![]() ,
,
综上所述,等腰三角形△DFG的腰长为4或20或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
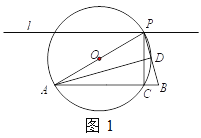
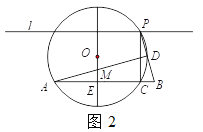
【题目】如图1,已知AB=8,直线l与AB平行,且l与AB的距离为4,P是l上的动点,过点P作PC ⊥AB,垂足为C,点C不与A,B重合,过A,C,P三点作⊙O.
(1)若⊙O与线段PB交于点D,∠PAD=22.5°,则∠APB等于多少度?
(2)如图2,⊙O与线段PB的一个公共点为D,一条直径垂直AB于点E,且与AD交于点M.
①若ME=![]() ,求AE的长;
,求AE的长;
②当ME的长度最大时,判断直线PB与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市经营的杂粮食物盒有A,B两种型号,单个盒子的容量和价格如下表所示,其中A型盒子正做促销活动:一次性购买三个及以上可返现8元.
型号 | A | B |
单个盒子的容量/升 | 4 | 6 |
单价/元 | 10 | 12 |
(1)张芳、王楠两人结伴去购物,请你根据两人的对话,判断怎样买最省钱:
张芳:“A型盒子有促销,我正好买几个装大米用,我买4个正好够用.”
王楠:“嗯,我也买几个,不过,我家得需要5个.”
张芳:“走,结账去.”
王楠:“等等,咱俩合计一下,怎么买最省钱…”
(2)小红和妈妈也来买盒子,下面是两人的对话:
妈妈:“这些盒子不错,买5个B型让孩子恰好能把咱家30升的小米都装上”
小红:“可是B型盒子没有折扣,咱可以两种盒子搭配着买,既能每个盒子都装满,还能省钱”
①设小红需要买A型号的盒子x个,一次性购买盒子的总费用为y元,求y与x的函数关系式;
②当x=3时,求小红和妈妈当天一次性购买盒子的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
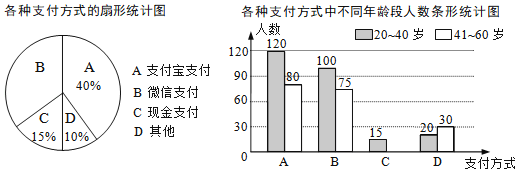
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产150辆自行车,平均每天生产辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比生产量最少的一天多生产 辆;
(3)该厂实行计划工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲同学在拼图探索活动中发现,用4个形状大小完全相同的直角三角形(直角边长分别为a,b,斜边长为c),可以拼成像如图1那样的正方形,并由此得出了关于a2,b2,c2的一个等式.
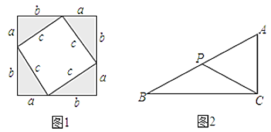
(1)请你写出这一结论:______,并给出验证过程.
(2)试用上述结论解决问题:如图2,P是Rt△ABC斜边AB上的一个动点,已知AC=5,AB=13,求PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)a5·(﹣a)3﹣(﹣2a2)4;
(2)[(x﹣2y)3]3÷[(2y﹣x)2]3
(3)﹣14﹣0.510×211+(![]() )0+3÷32
)0+3÷32
(4)(![]() )﹣1+50+[2﹣(﹣3)2]
)﹣1+50+[2﹣(﹣3)2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com