
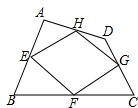
 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).分析 (1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=$\frac{1}{2}$BD,FG∥BD,FG═$\frac{1}{2}$BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)根据三角形的中位线定理和矩形的性质得出EF=FG=GH=EH即可得出结论.
解答 解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图1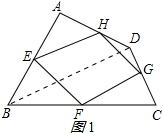 ,
,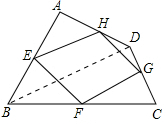 连结BD.
连结BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=$\frac{1}{2}$BD,
同理FG∥BD,FG=$\frac{1}{2}$BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
故答案为:平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图2,连结AC、BD.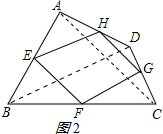
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案为:AC⊥BD;
(3)矩形的中点四边形是菱形.理由如下: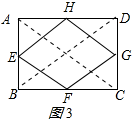
如图3,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH=$\frac{1}{2}$BD,FG=$\frac{1}{2}$BD,EF=$\frac{1}{2}$AC,GH=$\frac{1}{2}$AC,
∵四边形ABCD是矩形,
∴AC=BD,∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
点评 此题考查学生灵活运用三角形的中位线定理,平行四边形的判定及菱形的判定方法;熟记三角形中位线定理是解决问题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.5×10-13米 | B. | 15×10-6米 | C. | 1.5×10-5米 | D. | 1.5×10-6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
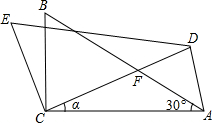 如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.
如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com