
【题目】如图,以直线![]() 上一点
上一点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将一个直角三角形的直角顶点放在点
,将一个直角三角形的直角顶点放在点![]() 处,(注,
处,(注,![]() )
)
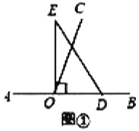
(1)如图①,若直角三角板![]() 的一边
的一边![]() 放在射线
放在射线![]() 上,则
上,则![]() ______°;
______°;
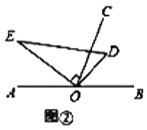
(2)如图②,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动到某个位置,若
逆时针方向转动到某个位置,若![]() 恰好平分
恰好平分![]() ,求
,求![]() 的度数;
的度数;
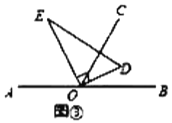
(3)如图③,将直角三角板![]() 绕点
绕点![]() 转动,如果
转动,如果![]() 始终在
始终在![]() 的内部,试猜想
的内部,试猜想![]() 和
和![]() 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.
【答案】(1)20;(2)![]() =20
=20![]() ;(3)∠COE∠BOD=20
;(3)∠COE∠BOD=20![]() ,理由见解析;
,理由见解析;
【解析】
(1)根据图形得出∠COE=∠DOE-∠BOC,代入求出即可;
(2)根据角平分线定义求出∠EOB=2∠BOC=140![]() ,代入∠BOD=∠BOE-∠DOE,求出∠BOD,代入∠COD=∠BOC-∠BOD求出即可;
,代入∠BOD=∠BOE-∠DOE,求出∠BOD,代入∠COD=∠BOC-∠BOD求出即可;
(3)根据图形得出∠BOD+∠COD=∠BOC=70![]() ,∠COE+∠COD=∠DOE=90
,∠COE+∠COD=∠DOE=90![]() ,相减即可求出答案.
,相减即可求出答案.
解:
(1)如图①,∠COE=∠DOE∠BOC=90![]() 70
70![]() =20
=20![]() ,
,
故答案为:20;
(2)如图②,
∵OC平分∠EOB∠BOC=70![]() ,
,
∴∠EOB=2∠BOC=140![]() ,
,
∵∠DOE=90![]() ,
,
∴∠BOD=∠BOE∠DOE=50![]() ,
,
∵∠BOC=70![]() ,
,
∴∠COD=∠BOC∠BOD=20![]() ;
;
(3)∠COE∠BOD=20![]() ,
,
理由是:如图③,
∵∠BOD+∠COD=∠BOC=70![]() ,∠COE+∠COD=∠DOE=90
,∠COE+∠COD=∠DOE=90![]() ,
,
∴(∠COE+∠COD)(∠BOD+∠COD)
=∠COE+∠COD∠BOD∠COD
=∠COE∠BOD
=90![]() 70
70![]()
=20![]() ,
,
即∠COE∠BOD=20![]() ;
;


科目:初中数学 来源: 题型:
【题目】已知△ABC,分别以BC,AB,AC为边作等边三角形BCE,ACF,ABD
(1)若存在四边形ADEF,判断它的形状,并说明理由.
(2)存在四边形ADEF的条件下,请你给△ABC添个条件,使得四边形ADEF成为矩形,并说明理由.
(3)当△ABC满足什么条件时四边形ADEF不存在.

查看答案和解析>>
科目:初中数学 来源: 题型:
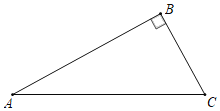
【题目】已知,如图,在直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8.P是线段AC上的一个动点,当点P从点C向点A运动时,运动到点A停止,设PC=x,△ABP的面积为y.求y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
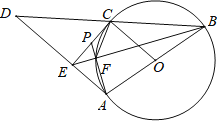
【题目】如图,AB为圆O的直径,C为圆O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.
(1)求证:直线EC为圆O的切线;
(2)设BE与圆O交于点F,AF的延长线与CE交于点P,已知∠PCF=∠CBF,PC=5,PF=4,求sin∠PEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com