
【题目】如图,![]() 的外角
的外角![]() 的平分线交
的平分线交![]() 边的垂直平分线于
边的垂直平分线于![]() 点,
点,![]() 于
于![]() ,
,![]() 于
于![]() .
.
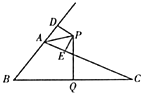
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)2
【解析】
(1)连接PB、PC,根据线段垂直平分线的性质得到PB=PC,根据角平分线的性质得到PD=PE,证明Rt△BPD≌Rt△CPE,根据全等三角形的性质证明;
(2)证明Rt△ADP≌Rt△AEP,得到AD=AE,根据题意列出方程,解方程即可.
(1)证明:连接PB、PC,
∵PQ是BC边的垂直平分线,
∴PB=PC,
∵AP平分∠DAC,PD⊥AB,PE⊥AC,
∴PD=PE,
在Rt△BPD和Rt△CPE中,
![]() ,
,
∴Rt△BPD≌Rt△CPE(HL),
∴BD=CE;
(2)在Rt△ADP和Rt△AEP中,
![]() ,
,
∴Rt△ADP≌Rt△AEP,
∴AD=AE,
∴AD+6=10AD,
解得,AD=2(cm).


科目:初中数学 来源: 题型:
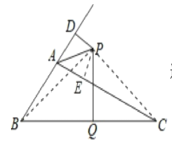
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
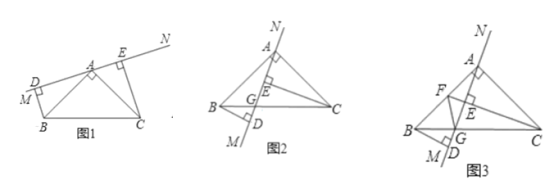
【题目】农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为_______m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。
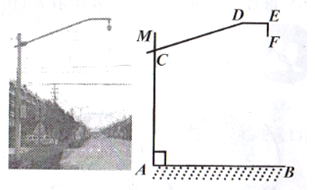
(1)求∠MCD的度数;
(2)求摄像头下端点F到地面AB的距离。(精确到百分位)
(参考数据;sin72°=0.95,cos72°≈0.31,tan72°=3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
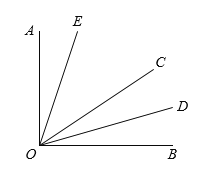
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,王老师把分别写有![]() ,5,-2,0,
,5,-2,0,![]() 的五张卡片分别发给
的五张卡片分别发给![]() 五位同学,王老师要求同学们按照卡片上数字的特征挑选2人或者3人表演节目.
五位同学,王老师要求同学们按照卡片上数字的特征挑选2人或者3人表演节目.
(1)王老师先给同学们做了范例,他说手拿卡片上数字为整数的同学表演节目,请你选出表演节目的同学;
(2)如果让你来挑选,你会按什么数字特征来选择表演节目的同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用棋子摆成一组“上”字:

如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第![]() 个、第
个、第![]() 个图形中的“上”字分别需要用多少枚棋子?
个图形中的“上”字分别需要用多少枚棋子?
(2)第![]() 个图形中的“上”字需要用多少枚棋子?
个图形中的“上”字需要用多少枚棋子?
(3)七(3)班有![]() 名同学,能否让这
名同学,能否让这![]() 名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
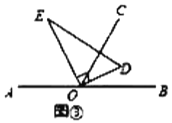
【题目】如图,以直线![]() 上一点
上一点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将一个直角三角形的直角顶点放在点
,将一个直角三角形的直角顶点放在点![]() 处,(注,
处,(注,![]() )
)
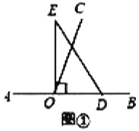
(1)如图①,若直角三角板![]() 的一边
的一边![]() 放在射线
放在射线![]() 上,则
上,则![]() ______°;
______°;
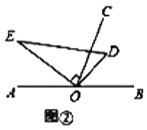
(2)如图②,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动到某个位置,若
逆时针方向转动到某个位置,若![]() 恰好平分
恰好平分![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,将直角三角板![]() 绕点
绕点![]() 转动,如果
转动,如果![]() 始终在
始终在![]() 的内部,试猜想
的内部,试猜想![]() 和
和![]() 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com