
【题目】如图,在![]() 中,
中,![]() 为
为![]() 上一点,以
上一点,以![]() 为圆心,
为圆心,![]() 长为半径作圆,与
长为半径作圆,与![]() 相切于点
相切于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
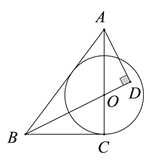
【答案】(1)证明见解析;(2)![]()
【解析】
(1)作OE⊥AB于点E,证明△OBC≌△OBE,根据全等三角形的对应边相等可得OE=OC, OE是⊙O的半径 ,OE⊥AB ,即可判定AB为⊙O的切线;
(2)根据题意先求出AO、BO的长,再证明△AOD∽△BOC,根据相似三角形对应边成比例即可求出AD的长.
(1)作OE⊥AB于点E,
∵![]() 切BC于点C,
切BC于点C,
∴OC⊥BC,∠ACB=90°,
∵ AD⊥BD,∴∠D=90°,
∴∠ABD+∠BAD =90°,∠CBD+∠BOC=90°,
∵∠BOC=∠AOD,∠AOD=∠BAD,
∴∠BOC=∠BAD,
∴∠ABD=∠CBD
在△OBC和△OBE中 ,
,
∴△OBC≌△OBE,
∴OE=OC,∴OE是⊙O的半径 ,
∵OE⊥AB ,∴AB为⊙O的切线;
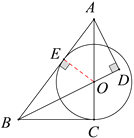
(2) ∵tan∠ABC=![]() ,BC=6,
,BC=6,
∴AC=8,∴AB=![]() ,
,
∵BE=BC=6,∴AE=4,
∵∠AOE=∠ABC,∴tan∠AOE=![]() ,∴EO=3,
,∴EO=3,
∴AO=5,OC=3,∴BO=![]() ,
,
在△AOD和△BOC中![]() ,
,
∴△AOD∽△BOC,∴![]() ,
,
即 ![]() ,∴AD=
,∴AD=![]() .
.


科目:初中数学 来源: 题型:
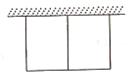
【题目】农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为_______m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,王老师把分别写有![]() ,5,-2,0,
,5,-2,0,![]() 的五张卡片分别发给
的五张卡片分别发给![]() 五位同学,王老师要求同学们按照卡片上数字的特征挑选2人或者3人表演节目.
五位同学,王老师要求同学们按照卡片上数字的特征挑选2人或者3人表演节目.
(1)王老师先给同学们做了范例,他说手拿卡片上数字为整数的同学表演节目,请你选出表演节目的同学;
(2)如果让你来挑选,你会按什么数字特征来选择表演节目的同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用棋子摆成一组“上”字:

如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第![]() 个、第
个、第![]() 个图形中的“上”字分别需要用多少枚棋子?
个图形中的“上”字分别需要用多少枚棋子?
(2)第![]() 个图形中的“上”字需要用多少枚棋子?
个图形中的“上”字需要用多少枚棋子?
(3)七(3)班有![]() 名同学,能否让这
名同学,能否让这![]() 名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
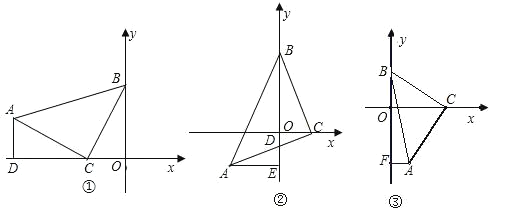
【题目】已知△ABC 是等腰直角三角形, BC AC ,ABC BAC ,直角顶点 C 在 x 轴上,一锐角顶点 B 在 y 轴上.
(1)如图①若 AD 于垂直 x 轴,垂足为点 D .点 C 坐标是 1, 0 ,点 A 的坐标是 3,1 , 求点 B 的坐标.
(2)如图②,直角边 BC 在两坐标轴上滑动,若 y 轴恰好平分 ABC , AC 与 y 轴交于点D ,过点 A 作 AE y 轴于 E ,请猜想 BD 与 AE 有怎样的数量关系,并证明你的猜想.
(3)如图③,直角边 BC 在两坐标轴上滑动,使点 A 在第四象限内,过 A 点作 AF y 轴于 F ,在滑动的过程中,两个结论①![]() 为定值;②
为定值;②![]() 为定值,只有一个结论成立,请你判断正确的结论加并求出定值.
为定值,只有一个结论成立,请你判断正确的结论加并求出定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是____.

①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
查看答案和解析>>
科目:初中数学 来源: 题型:
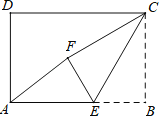
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=![]() ;
;
③当A、F、C三点共线时,AE=![]() ;
;
④当A、F、C三点共线时,△CEF≌△AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线![]() 上一点
上一点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将一个直角三角形的直角顶点放在点
,将一个直角三角形的直角顶点放在点![]() 处,(注,
处,(注,![]() )
)
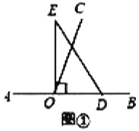
(1)如图①,若直角三角板![]() 的一边
的一边![]() 放在射线
放在射线![]() 上,则
上,则![]() ______°;
______°;
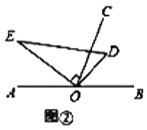
(2)如图②,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动到某个位置,若
逆时针方向转动到某个位置,若![]() 恰好平分
恰好平分![]() ,求
,求![]() 的度数;
的度数;
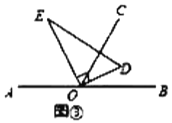
(3)如图③,将直角三角板![]() 绕点
绕点![]() 转动,如果
转动,如果![]() 始终在
始终在![]() 的内部,试猜想
的内部,试猜想![]() 和
和![]() 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
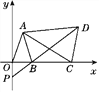
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com