
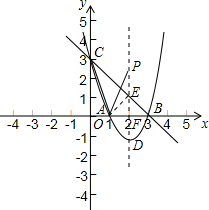
 在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B、C两点.
在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B、C两点.
|
|
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| AE |
| AF |
| CE |
| PF |
| ||
| 1 |
2
| ||
| PF |


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
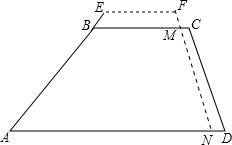 如图,一个防汛坝的横断面是梯形ABCD,坝顶BC的宽为10米,坝高为5米,斜坡AB的坡比i1=1:1.5,斜坡CD的坡比i2=1:0.8.一次由于上游突降大雨,造成河水迅速上涨,为了及时加高坝身,只能用坝身后一侧CD处的土临时加高,现决定将CD一侧宽1米的土方全部用来加高坝身,且使坝身两侧的坡度与原来保持一致.问这样能使坝高增加多少米?(精确到0.1米)
如图,一个防汛坝的横断面是梯形ABCD,坝顶BC的宽为10米,坝高为5米,斜坡AB的坡比i1=1:1.5,斜坡CD的坡比i2=1:0.8.一次由于上游突降大雨,造成河水迅速上涨,为了及时加高坝身,只能用坝身后一侧CD处的土临时加高,现决定将CD一侧宽1米的土方全部用来加高坝身,且使坝身两侧的坡度与原来保持一致.问这样能使坝高增加多少米?(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、-2 | B、-1 | C、0 | D、2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com