
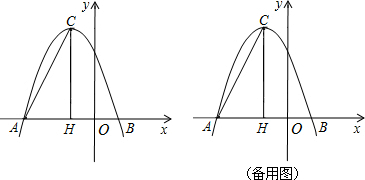
分析 (1)将A(-3,0)、B(1,0)代入y=ax2+bx+3求出即可,再利用平方法求出顶点坐标即可;
(2)首先证明△CED∽△DOA,得出y轴上存在点D(0,3)或(0,1),即可得出△ACD是以AC为斜边的直角三角形;
(3)首先求出直线CA的解析式为y=k1x+b1,再联立两函数解析式即可得出交点坐标,再利用若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH得出答案即可.
解答 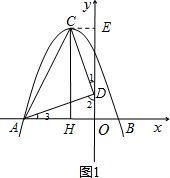 解:(1)把A(-3,0)、B(1,0)分别代入y=ax2+bx+3,得
解:(1)把A(-3,0)、B(1,0)分别代入y=ax2+bx+3,得
$\left\{\begin{array}{l}{0=9a-3b+3}\\{0=a+b+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$,
则该抛物线的解析式为:y=-x2-2x+3.
因为y=-x2-2x+3=-(x+1)2+4,
所以顶点C的坐标为(-1,4);
(2)如图1,假设在y轴上存在满足条件的点D,过点C作CE⊥y轴于点E.
由∠CDA=90°得∠1+∠2=90°.
又∵∠2+∠3=90°,
∴∠3=∠1,
又∵∠CED=∠DOA=90°,
∴△CED∽△DOA,
∴$\frac{CE}{ED}$=$\frac{DO}{AO}$.
设D(0,c),
则 $\frac{1}{4-c}$=$\frac{c}{3}$.
变形,得c2-4c+3=0,
解得c1=3,c2=1.
综合上述:在y轴上存在点D(0,3)或(0,1),使△ACD是以AC为斜边的直角三角形.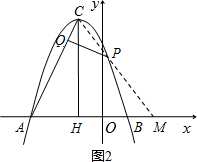
(3)①若点P在对称轴右侧(如图2),只能是△PCQ∽△CAH,得∠QCP=∠CAH.
延长CP交x轴于M,
∴AM=CM,
∴AM2=CM2.
设M(m,0),则(m+3)2=42+(m+1)2,
∴m=2,即M(2,0).
设直线CM的解析式为y=k1x+b1,
则 $\left\{\begin{array}{l}{-{k}_{1}+{b}_{1}=4}\\{2{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解之得$\left\{\begin{array}{l}{{k}_{1}=\frac{4}{3}}\\{{b}_{1}=\frac{8}{3}}\end{array}\right.$,
∴直线CM的解析式y=-$\frac{4}{3}$x+$\frac{8}{3}$.联立 $\left\{\begin{array}{l}{y=-\frac{4}{3}x+\frac{8}{3}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{20}{9}}\end{array}\right.$或 $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍去).
∴P($\frac{1}{3}$,$\frac{20}{9}$).
②若点P在对称轴左侧(如图3),只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.
由△CFA∽△CAH得 $\frac{CA}{AF}$=$\frac{CH}{AH}$=2,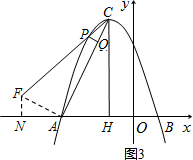
由△FNA∽△AHC得 $\frac{FN}{AH}$=$\frac{NA}{HC}$=$\frac{AF}{CA}$=$\frac{1}{2}$.
∴AN=2,FN=1,CH=4,HO=1,则AH=2,
∴点F坐标为(-5,1).
设直线CF的解析式为y=k2x+b2,则$\left\{\begin{array}{l}{-{k}_{2}+{b}_{2}=4}\\{-5{k}_{2}+{b}_{2}=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=\frac{3}{4}}\\{{b}_{2}=\frac{19}{4}}\end{array}\right.$.
∴直线CF的解析式y=$\frac{3}{4}$x+$\frac{19}{4}$.
联立$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{19}{4}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{7}{4}}\\{y=\frac{55}{16}}\end{array}\right.$或 $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍去).
∴P(-$\frac{7}{4}$,$\frac{55}{16}$).
∴满足条件的点P坐标为($\frac{1}{3}$,$\frac{20}{9}$)或(-$\frac{7}{4}$,$\frac{55}{16}$).
点评 此题主要考查了二次函数的综合应用以及相似三角形的应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.


科目:初中数学 来源: 题型:选择题
| A. | 多边形的外角和等于360° | |
| B. | 直角三角形的外角中可以有锐角 | |
| C. | 三角形两边之差小于第三边 | |
| D. | 如果两个角大小相等,且它们的和等于平角,那么这两个角都是直角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
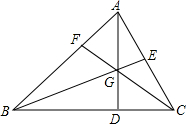 如图,在△ABC中,点D、E、F分别在三边上,点E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是30,△AGE的面积为3.
如图,在△ABC中,点D、E、F分别在三边上,点E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是30,△AGE的面积为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
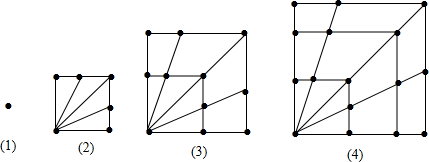
| A. | 32 | B. | 35 | C. | 36 | D. | 38 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com