

分析 奇数位置是矩形,偶数位置是菱形,第2014个四边形是菱形.根据第一个矩形的两条邻边长分别为3和4,得出中位线的长的长,再根据中位线定理,可知第一个菱形的边长是第一个矩形对应的对角线的$\frac{1}{2}$,即可得出第一个菱形的边长和周长,以次类推,即可得出第n个菱形的周长.
解答 解:因为第一个矩形的两条邻边长分别为3和4,
所以对角线的长为5,
根据中位线定理,可知第一个菱形的边长是第一个矩形对应的对角线的$\frac{1}{2}$,
所以第一个菱形的边长是$\frac{5}{2}$,周长是$\frac{5}{2}$×4=10,
因为第二个矩形的边长是第一个矩形对应的边长的$\frac{1}{2}$,
根据中位线定理,可知第二个菱形的边长是第二矩形对应的对角线的$\frac{1}{2}$,
所以第二个菱形的边长是$\frac{5}{2}$×$\frac{1}{2}$=$\frac{5}{4}$,周长是10×$\frac{1}{2}$=5,
同理:第三个菱形的周长为10×($\frac{1}{2}$)2,
所以第2014个菱形的周长为10×($\frac{1}{2}$)2013.
故答案为:10×($\frac{1}{2}$)2013.
点评 本题考查了图形的变化规律,用到的知识点是三角形的中位线定理及矩形、菱形的性质,是一道找规律的题目,这类题型在中考中经常出现.


科目:初中数学 来源: 题型:选择题
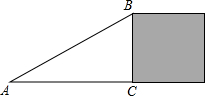 如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )
如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )| A. | 256cm | B. | 8cm | C. | 16cm | D. | 32cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
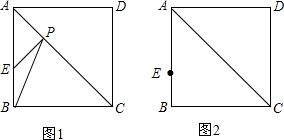 如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.
如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
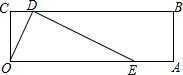 如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.
如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com