
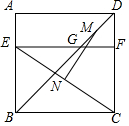
 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 4 |
分析 解法一:作辅助线,构建矩形MHPK和直角三角形NMH,利用平行线分线段成比例定理或中位线定理得:MK=FK=1,NP=3,PF=2,利用勾股定理可得MN的长;
解法二:作辅助线,构建全等三角形,证明△EMF≌△CMD,则EM=CM,利用勾股定理得:BD=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,EC=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,可得△EBG是等腰直角三角形,分别求EM=CM的长,利用勾股定理的逆定理可得△EMC是等腰直角三角形,根据直角三角形斜边中线的性质得MN的长.
解答 解:解法一:如图1,过M作MK⊥CD于K,过N作NP⊥CD于P,过M作MH⊥PM于H,
则MK∥EF∥NP,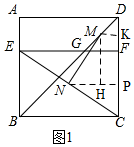
∵∠MKP=∠MHP=∠HPK=90°,
∴四边形MHPK是矩形,
∴MK=PH,MH=KP,
∵NP∥EF,N是EC的中点,
∴$\frac{CP}{PF}=\frac{CN}{EN}=1$,$\frac{NP}{EF}=\frac{CN}{EC}=\frac{1}{2}$,
∴PF=$\frac{1}{2}$FC=$\frac{1}{2}$BE=2,NP=$\frac{1}{2}$EF=3,
同理得:FK=DK=1,
∵四边形ABCD为正方形,
∴∠BDC=45°,
∴△MKD是等腰直角三角形,
∴MK=DK=1,NH=NP-HP=3-1=2,
∴MH=2+1=3,
在Rt△MNH中,由勾股定理得:MN=$\sqrt{N{H}^{2}+M{H}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
解法二:如图2,连接FM、EM、CM,
∵四边形ABCD为正方形,
∴∠ABC=∠BCD=∠ADC=90°,BC=CD,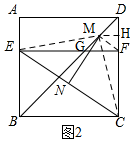
∵EF∥BC,
∴∠GFD=∠BCD=90°,EF=BC,
∴EF=BC=DC,
∵∠BDC=$\frac{1}{2}$∠ADC=45°,
∴△GFD是等腰直角三角形,
∵M是DG的中点,
∴FM=DM=MG,FM⊥DG,
∴∠GFM=∠CDM=45°,
∴△EMF≌△CMD,
∴EM=CM,
过M作MH⊥CD于H,
由勾股定理得:BD=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,
EC=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∵∠EBG=45°,
∴△EBG是等腰直角三角形,
∴EG=BE=4,
∴BG=4$\sqrt{2}$,
∴DM=$\sqrt{2}$
∴MH=DH=1,
∴CH=6-1=5,
∴CM=EM=$\sqrt{{1}^{2}+{5}^{2}}$=$\sqrt{26}$,
∵CE2=EM2+CM2,
∴∠EMC=90°,
∵N是EC的中点,
∴MN=$\frac{1}{2}$EC=$\sqrt{13}$;
故选C.
点评 本题考查了正方形的性质、三角形全等的性质和判定、等腰直角三角形的性质和判定、直角三角形斜边中线的性质、勾股定理的逆定理,属于基础题,本题的关键是证明△EMC是直角三角形.


科目:初中数学 来源: 题型:选择题
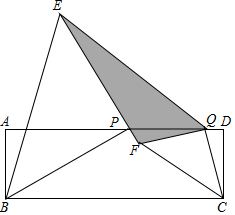 如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )
如图,矩形ABCD中,BC=6,P,Q是边AD上的动点,PQ=2,△BPE和△CQE均为等腰直角三角形(点B,P,E和C,Q,E均按逆时针顺序排列),∠BPE=∠CQF=Rt∠,则图中阴影部分的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1≤t≤$\frac{21}{4}$ | B. | -2≤t≤3 | C. | -1≤t<8 | D. | -2≤t<8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
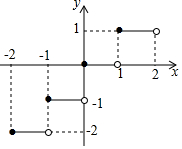 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )
定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )| A. | 0或$\sqrt{2}$ | B. | 0或2 | C. | 1或$-\sqrt{2}$ | D. | $\sqrt{2}$或-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
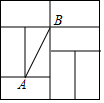 如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )
如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com