
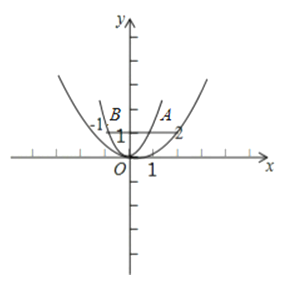
【题目】在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x﹣1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
(1)求点A,B的坐标.
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
【答案】
(1)
解:当y=2时,则2=x﹣1,
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(﹣1,2).
(2)
解:把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得:
![]()
解得:![]()
∴y=x2﹣2x﹣1.
顶点坐标为(1,﹣2).
(3)
解:如图,当C2过A点,B点时为临界,
代入A(3,2)则9a=2,
解得:a=![]() ,
,
代入B(﹣1,2),则a(﹣1)2=2,
解得:a=2,
∴![]() .
.
【解析】(1)当y=2时,则2=x﹣1,解得x=3,确定A(3,2),根据AB关于x=1对称,所以B(﹣1,2).
(2)把(3,2),(﹣2,2)代入抛物线C1:y=x2+bx+c得![]() ,求出b,c的值,即可解答;
,求出b,c的值,即可解答;
(3)画出函数图象,把A,B代入y=ax2 , 求出a的值,即可解答.
此题考查了二次函数的应用,利用待定系数法求参数值.


科目:初中数学 来源: 题型:
【题目】应用探究题 在图①中,已知长方形的长和宽分别为a,b,将线段A1A2向右平移1个单位长度到B1B2的位置,得到封闭图形A1A2B2B1(即阴影部分).
在图②中,将折线A1A2A3向右平移1个单位长度到折线B1B2B3的位置,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你画一条类似的有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出前三个图形中除去阴影部分后剩余部分的面积:S1,S2,S3;
(3)联想与探索:
如图④,在一块长方形草地上,草地的长和宽仍分别为a,b,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位长度),请你猜想空白部分表示的草地面积是多少,并说明你的猜想是正确的.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当k取不同的值时,y关于x的函数y=kx+2(k≠0)的图象为总是经过点(0,2)的直线,我们把所有这样的直线合起来,称为经过点(0,2)的“直线束”.那么,下面经过点(﹣1,2)的直线束的函数式是( )

A. y=kx﹣2(k≠0) B. y=kx+k+2(k≠0)
C. y=kx﹣k+2(k≠0) D. y=kx+k﹣2(k≠0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西绵山是中国历史文化名山,因春秋时期晋国介子推携母隐居于此被焚而著称,如图1,是绵山上介子推母子的塑像,某游客计划测量这座塑像的高度,由于游客无法直接到达塑像底部,因此该游客计划借助坡面高度来测量塑像的高度;如图2,在塑像旁山坡坡脚A处测得塑像头顶C的仰角为75°,当从A处沿坡面行走10米到达P处时,测得塑像头顶C的仰角刚好为45°,已知山坡的坡度i=1:3,且O,A,B在同一直线上,求塑像的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:cos75°≈0.3,tan75°≈3.7, ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈3.2)
≈3.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
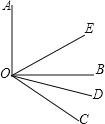
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC.
(1)如果∠AOB=900,∠BOC=400,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β (α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个布袋中装有只有颜色不同的a(a>12)个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整).请补全该统计图并求出 ![]() 的值.
的值. 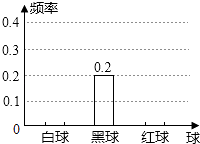
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com