
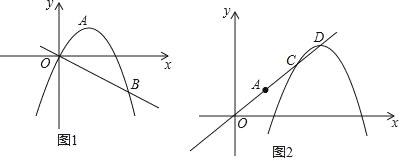
【题目】如图1,已知抛物线y=﹣x2+mx+m﹣2的顶点为A,且经过点B(3,﹣3).
(1)求顶点A的坐标
(2)若P是抛物线上且位于直线OB上方的一个动点,求△OPB的面积的最大值及比时点P的坐标;
(3)如图2,将原抛物线沿射线OA方向进行平移得到新的抛物线,新抛物线与射线OA交于C,D两点,请问:在抛物线平移的过程中,线段CD的长度是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)(﹣1,1);(2)P(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)过点P作y轴的平行线交OB与点Q,求出直线BP的解析式,表示出点Q的坐标,根据三角形的面积公式列出函数关系式,利用二次函数的最值可得P点坐标;
(3)根据平移规律,可得新抛物线,根据联立抛物线与OA的解析式,可得C、D点的横坐标,根据勾股定理,可得答案.
解:(1)把B(3,﹣3)代入y=﹣x2+mx+m2得:﹣3=﹣32+3m+m2,
解得m=2,
∴y=﹣x2+2x=﹣(x+1)2+1,
∴顶点A的坐标是(﹣1,1);
(2)过点P作y轴的平行线交OB与点Q.
∵直线OB的解析式为y=﹣x,
故设P(n,﹣n2+2n),Q(n,﹣n),
∴PQ=﹣n2+2n﹣(﹣n)=﹣n2+3n,
∴S△OPB=![]() (﹣n2+3n)=﹣
(﹣n2+3n)=﹣![]() (n﹣
(n﹣![]() )+
)+![]() ,
,
当n=![]() 时,S△OPB的最大值为
时,S△OPB的最大值为![]() .
.
此时y=﹣n2+2n=![]() ,
,
∴P(![]() ,
,![]() );
);
(3)∵直线OA的解析式为y=x,
∴可设新的抛物线解析式为y=﹣(x﹣a)2+a,
联立![]() ,
,
∴﹣(x﹣a)2+a=x,
∴x1=a,x2=a﹣1,
即C、D两点间的横坐标的差为1,
∴CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 两种机器人都被用来搬运化工原料,
两种机器人都被用来搬运化工原料,![]() 型机器人每小时搬运的化工原料是
型机器人每小时搬运的化工原料是![]() 型机器人每小时搬运的化工原料的1.5倍,
型机器人每小时搬运的化工原料的1.5倍,![]() 型机器人搬运900
型机器人搬运900![]() 所用时间比
所用时间比![]() 型机器人搬运800
型机器人搬运800![]() 所用时间少1小时.
所用时间少1小时.
(1)求两种机器人每小时分别搬运多少化工原料?
(2)某化工厂有8000![]() 化工原料需要搬运,要求搬运所有化工原料的时间不超过5小时,现计划先由6个
化工原料需要搬运,要求搬运所有化工原料的时间不超过5小时,现计划先由6个![]() 型机器人搬运3小时,再增加若干个
型机器人搬运3小时,再增加若干个![]() 型机器人一起搬运,请问至少要增加多少个
型机器人一起搬运,请问至少要增加多少个![]() 型机器人?
型机器人?
查看答案和解析>>
科目:初中数学 来源: 题型:
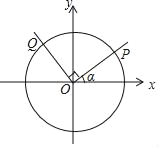
【题目】一般地,我们把半径为1的圆叫做单位圆,在平面直角坐标系xOy中,设单位圆的圆心与坐标原点O重合,则单位圆与x轴的交点分别为(1,0),(﹣1,0),与y轴的交点分别为(0,1),(0,﹣1).在平面直角坐标系xOy中,设锐角α的顶点与坐标原点O重合,α的一边与x轴的正半轴重合,另一边与单位圆交于点P(x1,y1),且点P在第一象限.
(1)求x1(用含α的式子表示);y1(用含α的式子表示);
(2)将射线OP绕坐标原点O按逆时针方向旋转90°后与单位圆交于点Q(x2,y2).
①判断y1与x2的数量关系,并证明;
②写出y1+y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人承包了一池塘养鱼,他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼,把每条鱼都作上标记,放回鱼塘;过了2天,他让他父亲从鱼塘内打捞上了50条鱼,结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤,平均每条鱼估计2.3斤,你能帮助他估计一下今年的收入情况吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同,小明先从盒子里随机取出一个小球,记下数字为x,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树形图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在二次函数y=x2的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
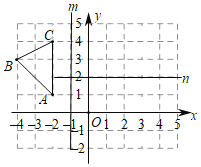
【题目】在直角坐标系中,△ABC的顶点坐标如图所示,
(1)请你在图中先作出△ABC关于直线m(直线m上点的横坐标均为﹣1)对称图形△A1B1C1,再作出△A1B1C1关于直线n(直线n上点的纵坐标均为2)对称图形△A2B2C2;
(2)线段BC上有一点M(a,b),点M关于直线m的对称点为N,点N关于直线的n的对称点为E,求N、E的坐标(用含a,b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
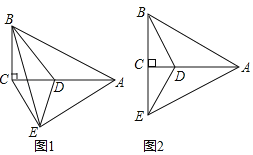
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,将△ABD沿BD(对称轴)翻折,点A落在点E处,连接AE,CE.
(1)如图1,当∠AEC=90°时,求证:CD=AD;
(2)当点E落在BC边所在直线上,且∠AEC=60°时.
①猜想△BAE是什么三角形并证明;
②试求线段CD、AD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
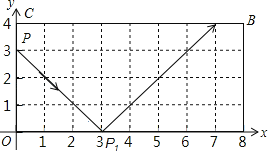
【题目】如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,点P2019的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com