
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.为了了解垃圾分类知识的普及情况,某校随机调查了部分学生,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制成下面两幅不完整的统计图:
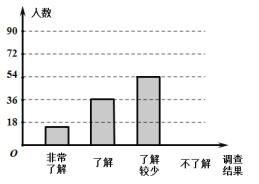
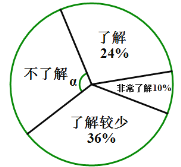
(1)本次被调查的学生有 名,扇形统计图中,![]()
(2)将条形统计图剩余的部分补充完整(包括朱标记的数据)
(3)估计该校![]() 名学生中“非常了解”与“了解”的人数和是多少.
名学生中“非常了解”与“了解”的人数和是多少.
(4)某环保小队有3名男生,1名女生,从中随机抽取2人在全校做垃圾分类知识交流,求恰好抽到一男一女的概率.
【答案】(1)![]() ;(2)见解析;(3)952;(4)树状图见解析,
;(2)见解析;(3)952;(4)树状图见解析,![]()
【解析】
(1)先由了解的人数及其所占百分比求出总人数,再根据各项目的百分比之和为1求出不了解对应的百分比,用360°乘以不了解对应的百分比可得答案;
(2)用总人数分别乘以非常了解、了解较少、不了解对应的百分比求出其人数,据此可补全图形;
(3)用总人数乘以两者百分比之和即可得;
(4)画树状图展示所有12种等可能的结果数,找出抽到一男一女的结果数,然后根据概率公式求解.
(1)本次被调查的学生有36÷24%=150(名),
∵“不了解”对应的百分比为1-(24%+10%+36%)=30%,
∴扇形统计图中,∠α=360°×30%=108°,
故答案为:150、108°;
(2)非常了解的人数为150×10%=15(名),
了解较少的人数为150×36%=54(名),
不了解的人数为150×30%=45(名),
补全图形如下:

![]() 估计该校
估计该校![]() 名学生中“非常了解”与“了解”的人数和是
名学生中“非常了解”与“了解”的人数和是![]() (名);
(名);
![]() 可以画树状图为:
可以画树状图为:
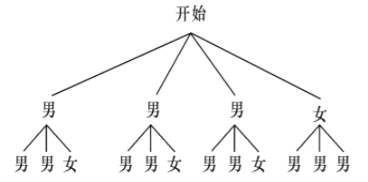
共有![]() 种等可能的结果,其中抽到
种等可能的结果,其中抽到![]() 男
男![]() 女的结果数为
女的结果数为![]()
所以恰好抽到一男一女的概率为![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
错误的个数有( )
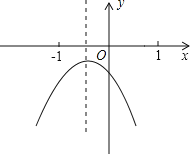
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
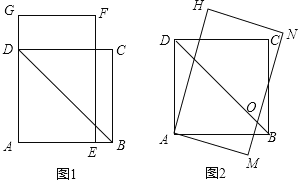
【题目】如图1,四边形ABCD是边长为![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
(1)求∠DOM的度数;
(2)图2中,求D、N两点间的距离;
(3)若将矩形AMNH绕点A再顺时针旋转15°得到矩形APQR,此时点B在矩形APQR的内部、外部还是边上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探究锐角三角函数的意义的学习过程中,小亮发现:“如图1,在![]() 中,
中,![]() ,可探究得到
,可探究得到![]() ”
”
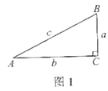
(1)请你利用图1探究说明小亮的说法是否正确;
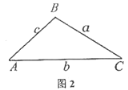
(2)小丽猜想“如果在钝角三角形中,两个锐角正弦值与它们所对边的边长之间也有一定的关系“在图2的钝角![]() 中,
中,![]() 是钝角,请你利用图2帮小丽探究
是钝角,请你利用图2帮小丽探究![]() 与
与![]() 之间的关系,并写出探究过程.
之间的关系,并写出探究过程.
(3)在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() 之间存在什么关系,请你探究并直接写出结论.
之间存在什么关系,请你探究并直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣![]() x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
A.﹣2B.﹣1C.1D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com