
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
错误的个数有( )
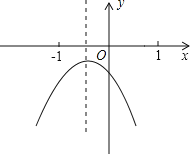
A.1个B.2个C.3个D.4个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
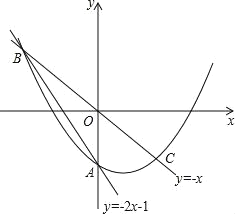
【题目】在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(Ⅰ)求过B,C两点的抛物线y=ax2+bx﹣1解析式;
(Ⅱ)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?最大值是多少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
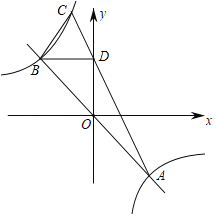
【题目】如图,反比例函数y=![]() (k≠0)与直线交于A,B两点.
(k≠0)与直线交于A,B两点.
(1)求证:OB=OA;
(2)连接CA交y轴于D点BD∥x轴,判断CB,CD的数量关系;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 与反比例函数
与反比例函数![]() (x>0)的图象交于点A.将
(x>0)的图象交于点A.将![]() 的图象向下平移6个单位后与双曲线
的图象向下平移6个单位后与双曲线![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
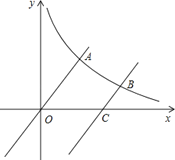
(1)求点C的坐标;
(2)若![]() ,求反比例函数的解析式.
,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机抽取了九年级部分学生进行体育模拟测试,将成绩统计分析并绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,绘制成如下所示的两幅统计图表(不完整的)
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |

请你根据图表中的信息完成下列问题:
(1)本次抽样调查的样本容量是 ,其中m= ,n= ;
(2)扇形统计图中E等级对应扇形的圆心角α= °;
(3)已知该校九年级共有700名学生,可以估计体育测试成绩在A、B两个等级的人数共有 人;
(4)该校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中随机选择2名作为代表参加全市体育交流活动,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.为了了解垃圾分类知识的普及情况,某校随机调查了部分学生,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制成下面两幅不完整的统计图:
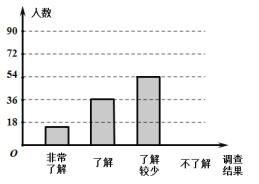
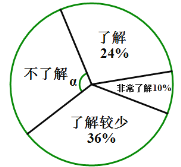
(1)本次被调查的学生有 名,扇形统计图中,![]()
(2)将条形统计图剩余的部分补充完整(包括朱标记的数据)
(3)估计该校![]() 名学生中“非常了解”与“了解”的人数和是多少.
名学生中“非常了解”与“了解”的人数和是多少.
(4)某环保小队有3名男生,1名女生,从中随机抽取2人在全校做垃圾分类知识交流,求恰好抽到一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com