
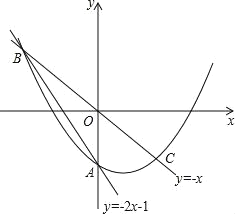
【题目】在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(Ⅰ)求过B,C两点的抛物线y=ax2+bx﹣1解析式;
(Ⅱ)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?最大值是多少?并说明理由.
【答案】(Ⅰ)抛物线解析式为y=x2﹣x﹣1;(Ⅱ)①P点坐标为(1﹣![]() ,1﹣
,1﹣![]() )或(1+
)或(1+![]() ,1+
,1+![]() );②当t=0时,四边形PBQC的面积最大,最大值为2,理由见解析.
);②当t=0时,四边形PBQC的面积最大,最大值为2,理由见解析.
【解析】
(Ⅰ)首先求出A、B、C三点坐标,再利用待定系数法可求得抛物线解析式;
(Ⅱ)①当四边形PBQC为菱形时,可知PQ⊥BC,则可求得直线PQ的解析式,联立抛物线解析式可求得P点坐标;
②过P作PD⊥BC,垂足为D,作x轴的垂线,交直线BC于点E,由∠PED=∠AOC,可知当PE最大时,PD也最大,用t可表示出PE的长,可求得取最大值时的t的值.
(Ⅰ)联立两直线解析式可得![]() ,
,
解得![]() ,
,
∴B点坐标为(﹣1,1),
又C点为B点关于原点的对称点,
∴C点坐标为(1,﹣1),
∵直线y=﹣2x﹣1与y轴交于点A,
∴A点坐标为(0,﹣1),
设抛物线解析式为y=ax2+bx+c,
把A、B、C三点坐标代入可得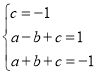 ,
,
解得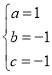 ,
,
∴抛物线解析式为y=x2﹣x﹣1;
(Ⅱ)①当四边形PBQC为菱形时,则PQ⊥BC,
∵直线BC解析式为y=﹣x,
∴直线PQ解析式为y=x,
联立抛物线解析式可得![]() ,
,
解得 或
或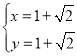 ,
,
∴P点坐标为(1﹣![]() ,1﹣
,1﹣![]() )或(1+
)或(1+![]() ,1+
,1+![]() );
);
②当t=0时,四边形PBQC的面积最大.
理由如下:
如图,过P作PD⊥BC,垂足为D,作x轴的垂线,交直线BC于点E,
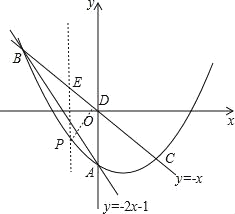
则S四边形PBQC=2S△PBC=2×![]() BCPD=BCPD,
BCPD=BCPD,
∵线段BC长固定不变,
∴当PD最大时,四边形PBQC面积最大,
又∠PED=∠AOC(固定不变),
∴当PE最大时,PD也最大,
∵P点在抛物线上,E点在直线BC上,
∴P点坐标为(t,t2﹣t﹣1),E点坐标为(t,﹣t),
∴PE=﹣t﹣(t2﹣t﹣1)=﹣t2+1,
∴当t=0时,PE有最大值1,此时PD有最大值,PD的最大值=![]() ,
,
∴四边形PBQC的面积最大值=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
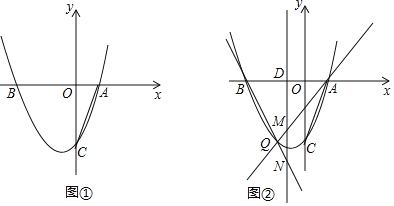
【题目】如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)如图①,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
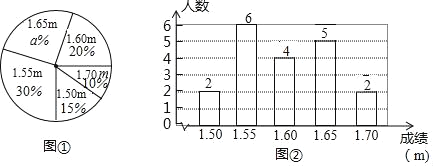
(Ⅰ)图①中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(Ⅲ)根据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
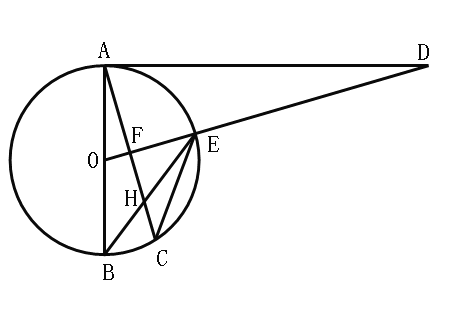
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,![]() 于点F,交⊙O于点E,AC交BE于点H,点D为OE延长线上的一点,且∠ODA=∠BEC.
于点F,交⊙O于点E,AC交BE于点H,点D为OE延长线上的一点,且∠ODA=∠BEC.
(1)求证:AD是⊙O的切线;
(2)求证:![]() ;
;
(3)若⊙O的半径为5,![]() ,求AH的长.
,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:

说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀);等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整):
c.乙企业样本数据的频数分布直方图如下:

d.两企业样本数据的平均数、中位数、众数、极差、方差如下:

根据以上信息,回答下列问题:
(1)![]() 的值为__________,
的值为__________,![]() 的值为______________;
的值为______________;
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为_____________;
若乙企业生产的某批产品共5万件,估计质量优秀的有_____________万件;
(3)根据图表数据,你认为___________企业生产的产品质量较好,理由为:__________________.(至少从两个角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市促销活动,将![]() 三种水果采用甲、乙、丙三种方式搭配装进礼盒进行销售.每盒的总成本为盒中
三种水果采用甲、乙、丙三种方式搭配装进礼盒进行销售.每盒的总成本为盒中![]() 三种水果成本之和,盒子成本忽略不计.甲种方式每盒分别装
三种水果成本之和,盒子成本忽略不计.甲种方式每盒分别装![]() 三种水果
三种水果![]() ;乙种方式每盒分别装
;乙种方式每盒分别装![]() 三种水果
三种水果![]() .甲每盒的总成本是每千克
.甲每盒的总成本是每千克![]() 水果成本的
水果成本的![]() 倍,每盒甲的销售利润率为
倍,每盒甲的销售利润率为![]() ;每盒甲比每盒乙的售价低
;每盒甲比每盒乙的售价低![]() ;每盒丙在成本上提高
;每盒丙在成本上提高![]() 标价后打八折出售,获利为每千克
标价后打八折出售,获利为每千克![]() 水果成本的
水果成本的![]() 倍.当销售甲、乙、丙三种方式搭配的礼盒数量之比为
倍.当销售甲、乙、丙三种方式搭配的礼盒数量之比为![]() 时,则销售总利润率为__________.
时,则销售总利润率为__________.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
错误的个数有( )
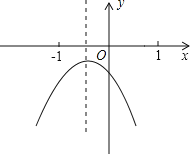
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com