
 设△ABC中,∠BAC=60°,∠ATC=∠BTC=∠BTA=120°,点M是BC的中点.求证:TA+TB+TC=2AM.
设△ABC中,∠BAC=60°,∠ATC=∠BTC=∠BTA=120°,点M是BC的中点.求证:TA+TB+TC=2AM. 分析 延长AM到K,使得MK=AM,连接BK,将△ATC绕点A逆时针旋转60°得到△AFE,连接TF.首先证明B、T、F、E共线,BE=BT+AT+TC,再证明△ABK≌△BAE,可得BE=AK=2AM,延长即可解决问题.
解答 证明:延长AM到K,使得MK=AM,连接BK,将△ATC绕点A逆时针旋转60°得到△AFE,连接TF.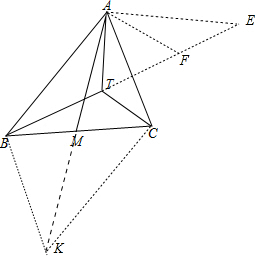
∵AT=AF,∠TAF=60°,
∴△ATF是等边三角形,
∴TA=TF,∠ATF=∠AFT=60°,
∵∠ATB=∠ATC=∠AFE=120°,
∴∠ATB+∠ATF=180°,∠AFT+∠AFE=180°,
∴B、T、F、E共线,
∴BE=BT+TF+EF=BT+AT+TC,
∵∠BAC=60°,
∴∠BAE=120°,
∵AM=MK,BM=MC,
∴四边形ABKC是平行四边形,
∴AC∥BK,
∴∠ABK+∠BAC=180°,
∴∠ABK=∠BAE=120°,
∵AB=BA,BK=AC=AE,
∴△ABK≌△BAE,
∴BE=AK=2AM,
∴TA+TB+TC=2AM.
点评 本题考查全等三角形的判定和性质、平行四边形的判定和性质、等边三角形的判定和性质等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,学会中线延长一倍构造全等三角形,题目有一定的难度.


科目:初中数学 来源: 题型:解答题
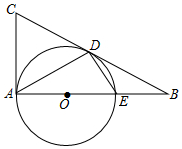 如图,在△ABC中,∠CAB=90°,点O在AB上,以OA为半径的⊙O与BC边相切于点D,与AB边相交于点E,连接AD、DE.
如图,在△ABC中,∠CAB=90°,点O在AB上,以OA为半径的⊙O与BC边相切于点D,与AB边相交于点E,连接AD、DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.
《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
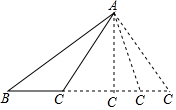 如图,△ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生变化,如果三角形的底边长为x(cm),三角形的面积y(cm2),那么y与x的关系可以表示为y=3x.
如图,△ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生变化,如果三角形的底边长为x(cm),三角形的面积y(cm2),那么y与x的关系可以表示为y=3x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com