
 《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.
《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.分析 (1)根据题意直接填空即可;
(2)根据题中所给的条件可知,竿斜放就恰好等于门的对角线长,可与门的宽和高构成直角三角形,运用勾股定理可求出门对角线长.
解答 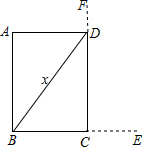 解:(1)由“横放,竿比门宽长出四尺”可得CE=4尺,
解:(1)由“横放,竿比门宽长出四尺”可得CE=4尺,
由“竖放,竿比门高长出二尺”可得DE=2尺,
故答案是:4;2;
(2)设户斜x尺,则图中BD=x.
BC=BE-CE=x-4(x>4)
CD=CF-DF=x-2(x>2)
又在直角三角形BCD中,∠BCD=90°,
由勾股定理得:BC2+CD2=BD2,
所以(x+4)2+(x-2)2=x2,
整理,得x2-12x+20=0,
因式分解,得(x-10)(x-2)=0,
解得x1=10,x2=2
因为x>4且x>2,
所以x=2舍去,x=10.
答:户斜为10尺.
点评 本题考查勾股定理的运用,正确运用勾股定理,将数学思想运用到实际问题中是解答本题的关键,难度一般.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
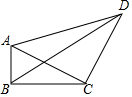 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5$\sqrt{2}$,则BD的长为$\sqrt{65}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com