
分析 (1)由DE∥BC,可得△ADE∽△ABC,又由△ADE的面积与四边形BCED的面积相等,根据相似三角形的面积比等于相似比的平方,即可解决问题;
(2)根据△ADE的周长与四边形BCED的周长相等,可得AE+AD=BC+CE+DB,不妨设AE+AD=a,CE+DB=b,由题意可得到a和b的方程组,解方程组可求出a的值,再根据相似三角形的性质即可求出DE的长.
解答 解:(1)解:∵DE∥BC,
∴△ADE∽△ABC,
∵△ADE的面积与四边形BCED的面积相等,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( $\frac{DE}{BC}$)2=$\frac{1}{2}$,
∴$\frac{DE}{BC}$=$\frac{1}{\sqrt{2}}$,
∴DE=3$\sqrt{2}$.
(2)解:∵△ADE的周长与四边形BCED的周长相等,
∴AD+AE+ED=BC+EC+DE+DB,即AE+AD=BC+CE+DB,
不妨设AE+AD=a,CE+DB=b,则 $\left\{\begin{array}{l}{a+b=11}\\{a-b=7}\end{array}\right.$,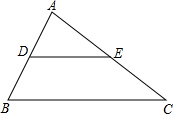
解得a=9,b=2
即AE+AD=9①,
∵DE∥BC,
∴△ADE∽△ACB,
∴$\frac{AE}{AD}$=$\frac{AC}{AB}$=$\frac{6}{5}$ ②,
由①②,得到AE=$\frac{54}{11}$,
∵$\frac{DE}{BC}$=$\frac{AE}{AC}$,
∴DE=$\frac{63}{11}$.
点评 此题考查了相似三角形的判定与性质、二元一次方程组等知识,解题的关键是注意相似三角形的面积比等于相似比的平方定理的应用,学会利用参数构建方程组,注意数形结合思想的应用.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
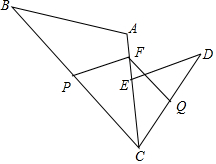 如图:E、A、C三点在同一条直线上,三角形ABC和三角形CDE是顶角相等的等腰三角形,其中BC和CD为等腰三角形的底边,F是AE的中点,P是BC边的中点,Q是CD边的中点.
如图:E、A、C三点在同一条直线上,三角形ABC和三角形CDE是顶角相等的等腰三角形,其中BC和CD为等腰三角形的底边,F是AE的中点,P是BC边的中点,Q是CD边的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,点A1,A2,A3,A4,…都在x轴上,点B1,B2,B3,…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A3A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2017的坐标为(22016,22016).
如图,在平面直角坐标系中,点A1,A2,A3,A4,…都在x轴上,点B1,B2,B3,…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A3A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2017的坐标为(22016,22016).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.
《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
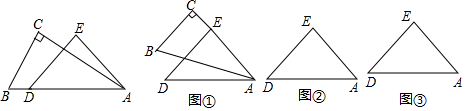
 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com