
【题目】.如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y. 则能够正确反映![]() 与
与![]() 之间的函数关系的图象是
之间的函数关系的图象是
A. 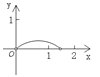 B.
B. 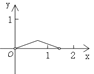 C.
C. 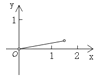 D.
D. 
【答案】A
【解析】
过点P作PF⊥BC于F,若要求△PBE的面积,则需要求出BE,PF的值,利用已知条件和正方形的性质以及勾股定理可求出BE,PF的值.再利用三角形的面积公式得到y与x的关系式,此时还要考虑到自变量x的取值范围和y的取值范围.
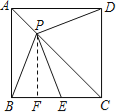
解:过点P作PF⊥BC于F,
∵PE=PB,
∴BF=EF,
∵正方形ABCD的边长是1,
∴AC=![]() =
=![]() ,
,
∵AP=x,∴PC=![]() -x,
-x,
∴PF=FC=![]() (
(![]() -x)=1-
-x)=1-![]() x,
x,
∴BF=FE=1-FC=![]() x,
x,
∴S△PBE=![]() BE?PF=
BE?PF=![]() x(1-
x(1-![]() x)=-
x)=-![]() x2+
x2+![]() x,
x,
即y=-![]() x2+
x2+![]() x(0<x<
x(0<x<![]() ),
),
∴y是x的二次函数(0<x<![]() ),
),
故选A.
本题考查了动点问题的函数图象,和正方形的性质;等于直角三角形的性质;三角形的面积公式.对于此类问题来说是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥AB于D,现有四个条件:①AD=ED ②∠A=∠BED ③∠C=∠B ④AC=EB,那么不能得出△ADC≌△EDB的条件是( ).
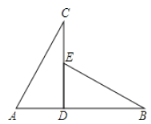
A.①③B.②④
C.①④D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1).
(2)利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 ,⊙P的半径= .(保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
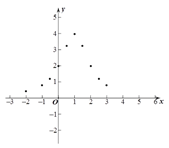
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, ![]() m)(m为非负数),则CA+CB的最小值是_____.
m)(m为非负数),则CA+CB的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象交
的图象交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和
和![]() ;另一个一次函数
;另一个一次函数![]() 的图象交
的图象交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和
和![]() ,且两个函数的图象交于点
,且两个函数的图象交于点![]()
(1)当![]() ,
,![]() 为何值时,
为何值时,![]() 和
和![]() 的图象重合;
的图象重合;
(2)当![]() 的面积为
的面积为![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com