
【题目】如图,已知CD⊥AB于D,现有四个条件:①AD=ED ②∠A=∠BED ③∠C=∠B ④AC=EB,那么不能得出△ADC≌△EDB的条件是( ).
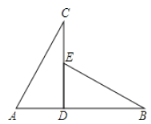
A.①③B.②④
C.①④D.②③
【答案】D
【解析】
推出∠ADC=∠BDE=90°,根据AAS推出两三角形全等,即可判断A、B;根据HL即可判断C;根据AAA不能判断两三角形全等.
解:A、∵CD⊥AB,∴∠ADC=∠BDE=90°,在△ADC和△EDB中,
∵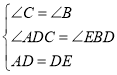 ,
,
∴△ADC≌△EDB(AAS),正确,故本选项错误;
B、∵CD⊥AB,∴∠ADC=∠BDE=90°,在△ADC和△EDB中,
∵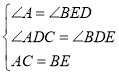 ,
,
∴△ADC≌△EDB(AAS),正确,故本选项错误;
C、∵CD⊥AB,∴∠ADC=∠BDE=90°,在Rt△ADC和Rt△EDB中,
∵![]() ,
,
∴Rt△ADC≌Rt△EDB(HL),正确,故本选项错误;
D、根据三个角对应相等,不能判断两三角形全等,错误,故本选项正确;
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,G是![]() 上一动点,AG,DC的延长线交于点F,连结BC.
上一动点,AG,DC的延长线交于点F,连结BC.
(1)若AB=4,∠B=60°,求![]() 的长;
的长;
(2)设∠DGF=![]() °,∠BCD=
°,∠BCD=![]() °,求
°,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造![]() 两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
型号 | 占地面积( | 使用农户数(户/个) | 造价(万元/个) |
|
|
|
|
|
|
|
|
已知可供建造沼气池的占地面积不超过![]() ,该村农户共有492户.
,该村农户共有492户.
(1)满足条件的方案共有几种?写出解答过程;
(2)通过计算判断,哪种建造方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A.抛掷一枚硬币,硬币落地时正面朝上是随机事件
B.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件
C.一个盒子中有白球![]() 个,红球6个,黑球
个,红球6个,黑球![]() 个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么
个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么![]() 与
与![]() 的和是6
的和是6
D.任意打开七年级下册数学教科书,正好是100页是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y. 则能够正确反映![]() 与
与![]() 之间的函数关系的图象是
之间的函数关系的图象是
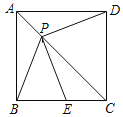
A. 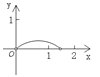 B.
B. 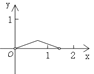 C.
C. 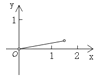 D.
D. 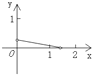
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,求BB′的长度.
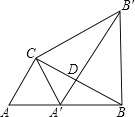
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,![]() 字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
字形是非常重要的基本图形,可以建立如下的“模块”(如图①):

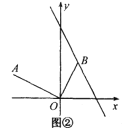

![]() .
.
(1)请就图①证明上述“模块”的合理性;
(2)请直接利用上述“模块”的结论解决下面两个问题:
①如图②,已知点![]() ,点
,点![]() 在直线
在直线![]() 上运动,若
上运动,若![]() ,求此时点
,求此时点![]() 的坐标;
的坐标;
②如图③,过点![]() 作
作![]() 轴与
轴与![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,求点
,求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com