
【题目】一次函数CD:![]() 与一次函数AB:
与一次函数AB:![]() ,都经过点B(-1,4).
,都经过点B(-1,4).
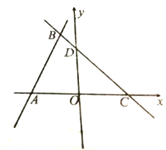
(1)求两条直线的解析式;
(2)求四边形ABDO的面积.
【答案】(1)直线CD的解析式为:![]() ;直线AB的解析式为:
;直线AB的解析式为:![]() ;
;
(2)四边形ABDO的面积为7.5.
【解析】
(1)将B(﹣1,4)代入一次函数CD:![]() 与一次函数AB:
与一次函数AB:![]() ,可以得到关于k、b的二元一次方程组,解方程组即可得到k、b的值,即可求出两条直线的解析式.
,可以得到关于k、b的二元一次方程组,解方程组即可得到k、b的值,即可求出两条直线的解析式.
(2)由图可知四边形ABDO不是规则的四边形,利用割补法得到![]() ,分别算出△ABC与△DOC的面积即可算出答案.
,分别算出△ABC与△DOC的面积即可算出答案.
解:(1)∵一次函数CD:![]() 与一次函数AB:
与一次函数AB:![]() ,都经过点B(﹣1,4),
,都经过点B(﹣1,4),
∴将点B(﹣1,4)代入一次函数CD:![]() 与一次函数AB:
与一次函数AB:![]() ,可得:
,可得:
![]() 解得:
解得:![]() ;
;
∴直线CD的解析式为:![]() ;直线AB的解析式为:
;直线AB的解析式为:![]() ;
;
(2)∵点A为直线AB与x轴的交点,令y=0得:![]() 解得:
解得:![]() ,
,
∴A(﹣3,0);
∵C为直线CD与x轴的交点,令y=0得:![]() 解得:
解得:![]() ,
,
∴C(3,0);
∵D为直线CD与y轴的交点,令x=0得y=3
∴D(0,3);
∴AC=6,OC=3,OD=3;
由图可知![]() ;
;
∴四边形ABDO的面积为7.5.


科目:初中数学 来源: 题型:
【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.
(千米)的函数图象.
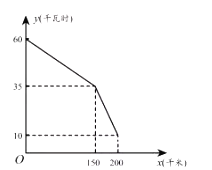
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当![]() 时,求1千瓦时的电量汽车能行驶的路程;
时,求1千瓦时的电量汽车能行驶的路程;
(2)当![]() 时求
时求![]() 关于
关于![]() 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的说理过程:如图,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 延长线上的点,连接
延长线上的点,连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .已知
.已知![]() ,
,![]() .对
.对![]() 和
和![]() 说明理由.
说明理由.

理由:![]() (已知),
(已知),
![]() (______),
(______),
![]() (等量代换).
(等量代换).
![]() (______).
(______).
![]() (______).
(______).
![]() (______),
(______),
![]() (______).
(______).
![]() (______).
(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市郊景区内一条笔直的公路![]() 经过
经过![]() 、
、![]() 两个景点,景区管委会又开发了风景优美的景点
两个景点,景区管委会又开发了风景优美的景点![]() ,经测量景点
,经测量景点![]() 位于景点
位于景点![]() 的北偏东
的北偏东![]() 方向,位于景点
方向,位于景点![]() 的正北方向,且景点
的正北方向,且景点![]() 位于景点
位于景点![]() 的北偏东
的北偏东![]() 方向,景点
方向,景点![]() 与景点
与景点![]() 距离为
距离为![]() .
.
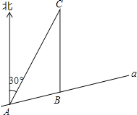
![]() 求景点
求景点![]() 与景点
与景点![]() 的距离;
的距离;
![]() 为方便游客到景点游玩,景区管委会准备由景点
为方便游客到景点游玩,景区管委会准备由景点![]() 向公路
向公路![]() 修建一条距离最短的公路,不考虑其它因素,求出这条公路的长.(结果保留根号)
修建一条距离最短的公路,不考虑其它因素,求出这条公路的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是边AC上一点,联结BD,给出下列条件:∠ABD=∠ACB;②AB2=ADAC;③ADBC=ABBD;④ABBC=ACBD.其中单独能够判定△ABD∽△ACB的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
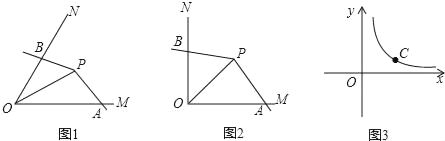
【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OAOB=OP2,我们就把∠APB叫做∠MON的智慧角.
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.
(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子表示∠APB的度数.
(3)如图3,C是函数![]() 图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣4,0),B (1,0)两点,与y轴交于点C.
(1)求这个二次函数的解析式;
(2)连接AC、BC,判断△ABC的形状,并证明;
(3)若点P为二次函数对称轴上点,求出使△PBC周长最小时,点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com