
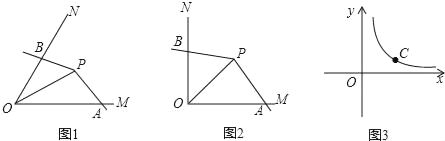
【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OAOB=OP2,我们就把∠APB叫做∠MON的智慧角.
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.
(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子表示∠APB的度数.
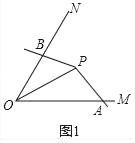
(3)如图3,C是函数![]() 图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
【答案】(1)详见解析;(2)∠APB=180°﹣![]() α;(3)点P的坐标为:(
α;(3)点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).
【解析】
(1)只要证明△AOP∽△POB,可得![]() =
=![]() ,即可证明;
,即可证明;
(2)由∠APB是∠MON的智慧角,可得![]() =
=![]() ,即可推出△AOP∽△POB,推出∠OAP=∠OPB,推出∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°-
,即可推出△AOP∽△POB,推出∠OAP=∠OPB,推出∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°-![]() α;
α;
(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;发三种情形情况:①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,如图3所示:②当点A在x轴的正半轴上时,如图4所示:③当点B在y轴的负半轴上时,如图5所示,分别求解即可.
(1)如图2中,
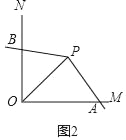
∵∠MON=90°,P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() ∠MON=45°,
∠MON=45°,
∵∠AOP+∠OAP+∠APO=180°,
∴∠OAP+∠APO=135°,
∵∠APB=135°,
∴∠APO+∠OPB=135°,
∴∠OAP=∠OPB,
∴△AOP∽△POB,
∴![]() ,
,
∴OP2=OAOB,
∴∠APB是∠MON的智慧角;
(2)如图1中,
∵∠APB是∠MON的智慧角,
∴OAOB=OP2,
∴![]() ,
,
∵P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() α,
α,
∴△AOP∽△POB,
∴∠OAP=∠OPB,
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°﹣![]() α,
α,
即∠APB=180°﹣![]() α;
α;
(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;分两种情况:
①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,如图3所示:
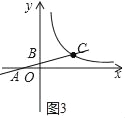
BC=2CA不可能;
②当点A在x轴的正半轴上时,如图4所示:
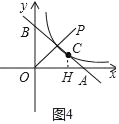
∵BC=2CA,
∴![]() ,
,
∵CH∥OB,
∴△ACH∽△ABO,
∴![]() ,
,
∴OB=3b,OA=![]() a,
a,
∴OAOB=![]() a3b=
a3b=![]() =
=![]() ,
,
∵∠APB是∠AOB的智慧角,
∴![]() ,
,
∵∠AOB=90°,OP平分∠AOB,
∴点P的坐标为:(![]() ,
,![]() );
);
③当点B在y轴的负半轴上时,如图5所示,
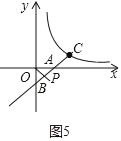
∵BC=2CA,
∴AB=CA,
在△ACH和△ABO中,
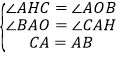 ,
,
∴△ACH≌△ABO(AAS),
∴OB=CH=b,OA=AH=![]() a,
a,
∴OAOB=![]() ab=
ab=![]() ,
,
∵∠APB是∠AOB的智慧角,
∴OP=![]() =
=![]() =
=![]() ,
,
∵∠AOB=90°,OP平分∠AOB,
∴点P的坐标为:(![]() ,
,![]() );
);
span>综上所述:点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是 ;
(2)据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、 92、85.
①这组数据的众数是 ,中位数是 ;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD,DE交BC于F,交AB的延长线于E,且∠EDB=∠C.
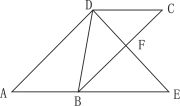
(1)求证:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
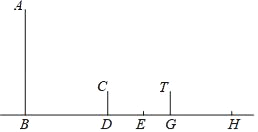
【题目】如图,花丛中有一路灯AB,在灯光下,小明在D点处的影长DE=3m,沿BD方向走到G点,DG=5m,这时,小明的影长GH=5m,小明的身高为1.7m.
(1)画出路灯灯泡A的位置.
(2)求AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
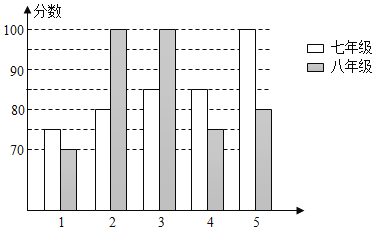
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
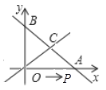
【题目】如图,已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() .点
.点![]() 从点
从点![]() 出发以每秒1个单位的速度向点
出发以每秒1个单位的速度向点![]() 运动,运动时间设为
运动,运动时间设为![]() 秒.
秒.
(1)求点![]() 的坐标;
的坐标;
(2)求下列情形![]() 的值;
的值;
①连结![]() ,
,![]() 把
把![]() 的面积平分;
的面积平分;
②连结![]() ,若
,若![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com