
【题目】如图1,点![]() 为直线
为直线![]() 上一点,将一副三角板如图摆放,其中两锐角顶点放在点
上一点,将一副三角板如图摆放,其中两锐角顶点放在点![]() 处,直角边
处,直角边![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上,且
上,且![]() ,
,![]() .
.
(1)将图1中的三角板![]() 绕点
绕点![]() 按逆时针方向旋转至图2的位置,使得
按逆时针方向旋转至图2的位置,使得![]() 落在射线
落在射线![]() 上,此时三角板
上,此时三角板![]() 旋转的角度为 度;
旋转的角度为 度;
(2)继续将图2中的三角板![]() 绕点O按逆时针方向旋转至图3的位置,使得
绕点O按逆时针方向旋转至图3的位置,使得![]() 在
在![]() 的内部,若
的内部,若![]() ,则
,则![]() 的度数为 度;
的度数为 度;
(3)在上述直角三角板![]() 从图l旋转到图3的位置的过程中,若三角板绕点
从图l旋转到图3的位置的过程中,若三角板绕点![]() 按每秒5°的速度旋转,当直角三角板
按每秒5°的速度旋转,当直角三角板![]() 的斜边
的斜边![]() 所在的直线恰好平分
所在的直线恰好平分![]() 时,求此时三角板
时,求此时三角板![]() 绕点
绕点![]() 的运动时间的值.
的运动时间的值.
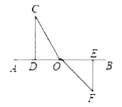
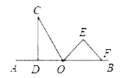
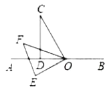
图1 图2 图3
【答案】(1)45;(2)20;(3)直角三角板![]() 的斜边
的斜边![]() 所在的直线恰好平分
所在的直线恰好平分![]() 时,三角板
时,三角板![]() 绕点
绕点![]() 的运动时间的值为3或39秒
的运动时间的值为3或39秒
【解析】
(1)∠EOB的度数就是旋转的角度;
(2)先求出∠AOF的度数,则∠AOE=∠EOF-∠AOF可求解;
(3)分情况讨论:①OF平分∠DOC;②OF反向延长线平分∠DOC,分别求出两种情况下旋转的度数,再除以旋转速度便可得时间.
解:(1)![]() ,
,
![]() 落在射线
落在射线![]() 上时,
上时,![]() 旋转的角度是45°,
旋转的角度是45°,
![]() 三角板
三角板![]() 旋转的角度为45°,
旋转的角度为45°,
故答案为:45;
(2)20.
由图3可知,![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
(3)①当![]() 的反向延长线平分
的反向延长线平分![]() 时,
时,
![]() 旋转的度数为:
旋转的度数为:![]() ,
,
![]() 直角三角板
直角三角板![]() 旋转的度数为:
旋转的度数为:![]() ,
,
则![]() 秒,
秒,
②当![]() 平分
平分![]() 时,
时,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() 直角三角板
直角三角板![]() 旋转的度数为:
旋转的度数为:![]() ,
,
则![]() 秒,
秒,
答:直角三角板![]() 的斜边
的斜边![]() 所在的直线恰好平分
所在的直线恰好平分![]() 时,三角板
时,三角板![]() 绕点
绕点![]() 的运动时间的值为3或39秒.
的运动时间的值为3或39秒.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
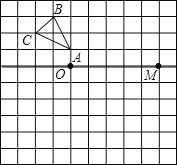
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O,M也在格点上.
(1)画出△ABC先向右平移5个单位长度,再向下平移5个单位长度得到的△A'B'C';
(2)画出△ABC关于直线OM对称的△A1B1C1;
(3)画出△ABC绕点O按顺时针方向旋转90°后所得的△A2B2C2;
(4)△A1B1C1与△A2B2C2组成的图形是轴对称图形吗?如果是轴对称图形,请画出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是矩形,已知PB=PC.
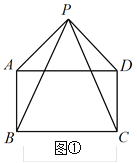
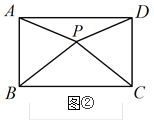
(1)若P是矩形外一点,求证:PA=PD;
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程|x2﹣x|﹣a=0,给出下列四个结论:①存在实数a,使得方程恰有2个不同的实根; ②存在实数a,使得方程恰有3个不同的实根;③存在实数a,使得方程恰有4个不同的实根;④存在实数a,使得方程恰有6个不同的实根;其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
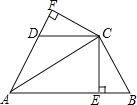
(1)BE与DF是否相等?请说明理由;
(2)若DF=1,AD=3,求AB的长;
(3)若△ABC的面积是23,△ADC面积是18,直接写出△BEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个有理数都能写成分数的形式(整数可以看作是分母为1的分数).我们知道:0.12可以写![]() ,0.123可以写成
,0.123可以写成![]() ,因此,有限小数是有理数那么无限循环小数是有理数吗?下面以循环小数2.61545454…=
,因此,有限小数是有理数那么无限循环小数是有理数吗?下面以循环小数2.61545454…=![]() 为例,进行探索:
为例,进行探索:
设x=![]() ,①
,①
两边同乘以100得:100x=![]() ,②
,②
②-①得:99x=261.54-![]() =258.93,
=258.93,
∴x=![]()
因此, ![]() 是有理数.
是有理数.
(1)直接用分数表示循环小数![]() =______.
=______.
(2)试说明![]() 是一个有理数,即能用一个分数表示.
是一个有理数,即能用一个分数表示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com