
分析 此题根据△ABC中∠A为锐角与钝角,分为两种情况解答,由线段垂直平分线的性质与等腰三角形的性质即可求得答案.
解答 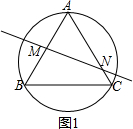 解:当∠A 为锐角时,如图1,
解:当∠A 为锐角时,如图1,
∵MN是AB的垂直平分线,
∴∠AMN=90°,
∵∠ANM=70°,
∴∠A=20°,
∵AB=AC,
∴∠B=80°,
∴劣弧$\widehat{AC}$所对的圆心角的度数为:160°;
当∠A为钝角时,如图2,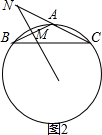
∵MN是AB的垂直平分线,
∴∠AMN=90°,
∵∠ANM=70°,
∴∠BAN=20°,
∴∠BAC=160°,
∵AB=AC,
∴∠B=10°,
∴劣弧$\widehat{AC}$所对的圆心角的度数为:20°,
故答案为:160°或20°.
点评 本题考查的是三角形的外接圆与外心,线段垂直平分线的性质以及等腰三角形的性质,此类题需要注意的是要分两种情况解答,考生在考虑问题时要全面.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
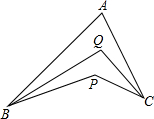 已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示)
已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
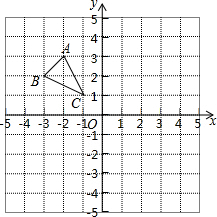 已知△ABC在平面直角坐标系中的位置如图所示
已知△ABC在平面直角坐标系中的位置如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com