
分析 将两式系数取各系数的最小公倍数,相同因式的次数取最高次幂,找出公因式,再进行变形即可.
解答 解:(1)$\frac{2a}{-3ab}$=-$\frac{10{a}^{2}c}{15{a}^{2}bc}$,$\frac{b}{15{a}^{2}bc}$;
(2)$\frac{2xy}{(x+y)^{2}}$=$\frac{2xy(x-y)}{(x+y)^{2}(x-y)}$,$\frac{x}{{x}^{2}-{y}^{2}}$=$\frac{x(x+y)}{(x+y)^{2}(x-y)}$;
(3)$\frac{1}{2{a}^{2}b}$=$\frac{6b{c}^{2}}{12{a}^{2}{b}^{2}{c}^{2}}$,$\frac{3}{4a{b}^{2}}$=$\frac{9a{c}^{2}}{12{a}^{2}{b}^{2}{c}^{2}}$,$\frac{5}{6a{c}^{2}}$=$\frac{10a{b}^{2}}{12{{a}^{2}b}^{2}{c}^{2}}$;
(4)$\frac{1}{x-1}$=$\frac{x+1}{(x+1)(x-1)}$,$\frac{1}{x+1}$=$\frac{x-1}{(x+1)(x-1)}$,$\frac{3x}{{x}^{2}-1}$=$\frac{3x}{(x+1)(x-1)}$.
点评 此题考查了通分,解答此题的关键是熟知找公分母的方法:
(1)系数取各系数的最小公倍数;
(2)凡出现的因式都要取;
(3)相同因式的次数取最高次幂.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
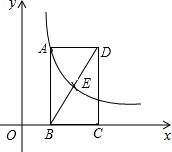 如图,矩形ABCD的边BC在x轴上,E是对角线BD的中点,点E的横坐标为m,A、E是函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,且该函数图象经过点(1,3).
如图,矩形ABCD的边BC在x轴上,E是对角线BD的中点,点E的横坐标为m,A、E是函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,且该函数图象经过点(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
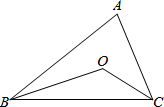 如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答:
如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com