
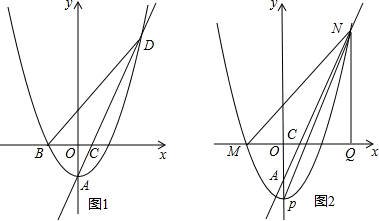
���� ��1�����ݵ�AC����������ֱ��AC�Ľ���ʽ���������߷���Ϊ����ʽy=ax2-2��a��0����Ȼ��ѵ�A�������������a��ֵ���ɣ�
��2������������ֱ�߽�����õ���D������Ϊ��4��6������DE��x����H����OH=4����EF��y�ᣬ��ֱ��AD��F����ϡ��ָ�����������ε�������н����Ҫ�������ۣ���E��ֱ��AD�·�ʱ��0��t��4���͵�E��ֱ��AD�Ϸ������������E������ꣻ
��3�����������ߵ�ƽ�ƹ��ɵõ�������L2�Ľ���ʽΪy=$\frac{1}{2}$x2-2-m�����������ͼ���������MQ=NQ���ɴ�֤�ý��ۣ�
����ֱ��MN��y����T������N��NH��y���ڵ�H���ɽ�ƽ���ߵ����ʺ͵��������ε��ж���֪����MOT����NHT��Ϊ����ֱ�������Σ���ϵ���ֱ�������ε������г�����m�ķ���$\sqrt{2}$��2+$\sqrt{2m+4}$��=$\sqrt{2m+4}$+m+2�����û�Ԫ�����m��ֵ���ɣ�
��� 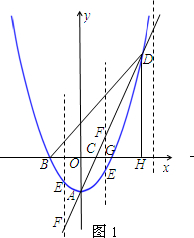 �⣺��1����ͼ1����ֱ��AC�Ľ���ʽΪy=kx+b��k��0����
�⣺��1����ͼ1����ֱ��AC�Ľ���ʽΪy=kx+b��k��0����
��A��0��-2����C��1��0�����룬��
$\left\{\begin{array}{l}{b=-2}\\{0=k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=2}\\{b=-2}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=2x-2��
�������߷���Ϊy=ax2-2��a��0����
��B��-2��0�����룬��
0=4a-2��a=$\frac{1}{2}$��
��������L1��y=$\frac{1}{2}$x2-2��
��2����$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-2}\\{y=2x-2}\end{array}\right.$ ���$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=6}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=0}\\{{y}_{2}=-2}\end{array}\right.$����ȥ����
���D��������4��6����
��S��OBD=6��
��S��EAD=3��
��ͼ1����DH��x����H����OH=4��
��EF��y�ᣬ��ֱ��AD��F��
��E��t��$\frac{1}{2}$t2-2������F��t��2t-2����
��E��ֱ��AD�·�ʱ��0��t��4����EF=2t-$\frac{1}{2}$t2��
S��EAD=S��EFA+S��EFD=$\frac{1}{2}$EF•OG+$\frac{1}{2}$EF•GH=$\frac{1}{2}$EF•OH=2��2t-$\frac{1}{2}$t2��=3��
���t=1��t=3��
��E��1��-$\frac{3}{2}$����3��$\frac{5}{2}$����
��E��ֱ��AD�Ϸ�ʱ��t��0��t��4����EF=$\frac{1}{2}$t2-2t��
��t��0ʱ��S��EAD=S��EFD-S��EFA=$\frac{1}{2}$EF•OH=2��$\frac{1}{2}$t2-2t��=3��
��t��4ʱ��S��EAD=S��EFA-S��EFD=$\frac{1}{2}$EF•OH=2��$\frac{1}{2}$t2-2t��=3��
��� t=2��$\sqrt{7}$��
��E��2+$\sqrt{7}$��$\frac{7}{2}$+2$\sqrt{7}$����2-$\sqrt{7}$��$\frac{7}{2}$-2$\sqrt{7}$����
���ϣ�E������Ϊ����1��-$\frac{3}{2}$����3��$\frac{5}{2}$����2+$\sqrt{7}$��$\frac{7}{2}$+2$\sqrt{7}$����2-$\sqrt{7}$��$\frac{7}{2}$-2$\sqrt{7}$����
��3����������L2�Ľ���ʽΪy=$\frac{1}{2}$x2-2-m��
��P��0��-2-m����M��-$\sqrt{2m+4}$��0����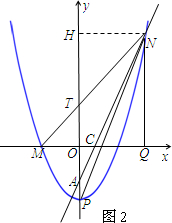
��$\left\{\begin{array}{l}{y=2x-2}\\{y=\frac{1}{2}{x}^{2}-2-m}\end{array}\right.$ ��N��2+$\sqrt{2m+4}$��2+2$\sqrt{2m+4}$����
��Q��2+$\sqrt{2m+4}$��0����
��MQ=2+$\sqrt{2m+4}$+$\sqrt{2m+4}$+=2+2$\sqrt{2m+4}$=NQ��
���NMQ=45�㣻
����ͼ2����ֱ��MN��y����T������N��NH��y���ڵ�H��
��PNƽ�֡�MNQ��NQ��TP
���MNP=��PNQ=��TPN��
��PT=NT��
�ߡ�MQT����NHT��Ϊ����ֱ�������Σ�
��MQ=NQ��HT=HN��
��NT=$\sqrt{2}$NH��PT=TO+OP=OM+OP
��$\sqrt{2}$��2+$\sqrt{2m+4}$��=$\sqrt{2m+4}$+m+2
��$\sqrt{m+2}$=t����t2+��$\sqrt{2}$-2��t-2$\sqrt{2}$=0��
���t=2��t=-$\sqrt{2}$����ȥ����
��$\sqrt{m+2}$=2��
��m=2��
���� ���⿼���˶��κ����Ľ���ʽ��������ֱ�������ε��ж������ʵ��ۺ�����������Ҫ���������ν�ϵ�˼��Ѵ����ͼ���ͼ�ν�����������õ������������ʾ�߶εij��ȣ��Ӷ�����߶�֮��Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
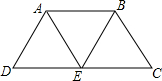 �ı���ABCD�У�DC��AB��DC=2AB��EΪDC���е㣬����AE��EB
�ı���ABCD�У�DC��AB��DC=2AB��EΪDC���е㣬����AE��EB�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
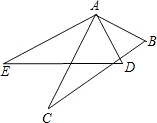 ��ͼ����֪��ABC�ա�ADE��B��D��C��E�Ƕ�Ӧ���㣬��ôBC�Ķ�Ӧ����DE��
��ͼ����֪��ABC�ա�ADE��B��D��C��E�Ƕ�Ӧ���㣬��ôBC�Ķ�Ӧ����DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ϣ�ֱ��x=3 | B�� | ���£�ֱ��x=3 | C�� | ���ϣ�ֱ��x=-3 | D�� | ���£�ֱ��x=-3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com