
分析 根据关于a的一元二次方程2a2+8a=k有两个相等的实数根,可以求得k和a的值,然后代入分式方程$\frac{x}{x-1}$+k+3=$\frac{a+5}{1-x}$,从而可以求得分式方程的解.
解答 解:∵关于a的一元二次方程2a2+8a=k有两个相等的实数根,
∴2a2+8a-k=0,
∴82-4×2×k=0,${a}_{1}={a}_{2}=\frac{-8}{2×2}=-2$,
解得,k=8,
∴k=8,a=-2,
∴$\frac{x}{x-1}$+k+3=$\frac{a+5}{1-x}$可以变形为:$\frac{x}{x-1}+8+3=\frac{-2+5}{1-x}$,
化简,得$\frac{x}{x-1}+11=\frac{3}{1-x}$,
解得,x=$\frac{2}{3}$,
经检验,x=$\frac{2}{3}$是原分式方程的解,
即关于x的分式方程$\frac{x}{x-1}$+k+3=$\frac{a+5}{1-x}$的解是x=$\frac{2}{3}$.
点评 本题考查根的判别式、解分式方程,解题的关键是明确题意,找出所求问题需要的条件,注意分式方程最好要检验.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
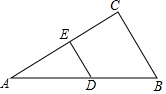 如图,在△ABC中,AB=8,∠C=90°,∠A=30°,D、E分别为AB、AC边上的中点,则DE的长为( )
如图,在△ABC中,AB=8,∠C=90°,∠A=30°,D、E分别为AB、AC边上的中点,则DE的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 3 |
| A. | 18,19 | B. | 19,19 | C. | 18,19.5 | D. | 19,19.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -22=4 | B. | (-2)3=-6 | C. | ${(-\frac{1}{2})^3}=-\frac{1}{8}$ | D. | ${({-2\frac{1}{3}})^3}=-8\frac{1}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com