
 填空,完成下列说理过程
填空,完成下列说理过程分析 (1)由已知条件和观察图形,再利用角平分线的性质就可求出角的度数;
(2)由已知条件和观察图形,再利用角平分线的性质就可求出角的度数.
解答 解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=$\frac{1}{2}$∠AOC.
因为OE是∠BOC的平分线,
所以∠COE=$\frac{1}{2}$∠BOC.
所以∠DOE=∠COD+∠COE=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB=90°.
(2)由(1)可知
∠BOE=∠COE=∠DOE-∠COD=25°,
所以∠AOE=∠AOB-∠BOE=155°.
故答案为(1)∠COE;∠COE;90;(2)∠DOE(或者90°);25;∠AOB(或者180°);155.
点评 此题主要考查了垂线和角平分线的定义,要注意领会由两角和为90°得互余这一要点.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
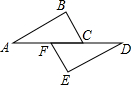 如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )
如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )| A. | ∠A=∠D | B. | AB=FD | C. | AC=ED | D. | AF=CD |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
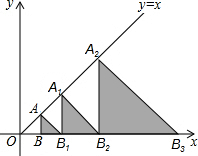 如图,点A,A1,A2,…都在直线y=x上,点B,B1,B2,B3,…都在x轴上,且△ABB1,△A1B1B2,△A2B2B3,…都是等腰直角三角形,若按如此规律排列下去,已知B(1,0),则A2016的坐标为(22016,22016).
如图,点A,A1,A2,…都在直线y=x上,点B,B1,B2,B3,…都在x轴上,且△ABB1,△A1B1B2,△A2B2B3,…都是等腰直角三角形,若按如此规律排列下去,已知B(1,0),则A2016的坐标为(22016,22016).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=8,OE=4.求该反比例函数的解析式.
已知:如图,在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=8,OE=4.求该反比例函数的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com