
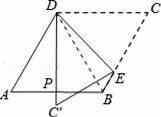
如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )


A.78° B.75° C.60° D.45°
B【考点】翻折变换(折叠问题);菱形的性质.
【分析】连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.
【解答】解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
在△DEC中,∠DEC=180°﹣(∠CDE+∠C)=75°.
故选:B.



 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
下列事件中,是必然事件的为( )
A.3天内会下雨
B.打开电视机,正在播放广告
C.367人中至少有2人公历生日相同
D.某妇产医院里,下一个出生的婴儿是女孩
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下面的变形规律:
 =1﹣
=1﹣
 ,
,
 =
=
 ﹣
﹣
 ,
,
 =
=
 ﹣
﹣
 ,…
,…
解答下面的问题:
(1)若n为正整数,请你猜想
 = ;
= ;
(2)证明你猜想的结论;
(3)计算:
 +
+
 +
+
 +…+
+…+
 +
+
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了了解某校八年级1000名学生的身高,从中抽取了50名学生并对他们的身高进行统计分析,以下说法正确的是( )
A.1 000名学生是总体
B.抽取的50名学生是样本容量
C.每位学生的身高是个体
D.被抽取的50名学生是总体的一个样本
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com