
ĄŸÌâÄżĄżÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹ”ăC”ÄŚű±êÎȘŁš0ŁŹ1.5Ł©ŁŹÎÒĂÇ°ŃÒÔ”ăCÎȘÔČĐÄŁŹ°ëŸ¶ÎȘ1.5”ÄÔČłÆÎȘ”ăC”ÄĆóÓŃÈŠŁŹÔČÖÜÉÏ”ÄĂżÒ»žö”ăœĐŚö”ăC”ÄÒ»žöșĂÓŃŁź
Łš1Ł©ĐŽłö”ăC”ÄÁœžöșĂÓŃŚű±êŁ»
Łš2Ł©Ö±Ïßl”ÄœâÎöÊœÊÇy=![]() x©4ŁŹÓëxÖ᥹yÖá·Ö±đœ»ÓÚAĄąBÁœ”㣏ÔČĐÄCŽÓ”㣚0ŁŹ1.5Ł©żȘÊŒÒÔĂżĂë0.5žö”„λ”ÄËÙ¶ÈŃŰŚĆyÖáÏòÏÂÔ˶ŻŁŹ”±”ăC”ÄĆóÓŃÈŠÓĐșĂÓŃÂäÔÚÖ±ÏßÉÏʱŁŹÖ±Ïßœ«ÊÜÆäÓ°ÏìŁŹÇóÔÚ”ăCÏòÏÂÔ˶Ż”ÄčęłÌÖĐŁŹÖ±ÏßÊÜÆäÓ°Ïì”ÄʱŒäŁ»
x©4ŁŹÓëxÖ᥹yÖá·Ö±đœ»ÓÚAĄąBÁœ”㣏ÔČĐÄCŽÓ”㣚0ŁŹ1.5Ł©żȘÊŒÒÔĂżĂë0.5žö”„λ”ÄËÙ¶ÈŃŰŚĆyÖáÏòÏÂÔ˶ŻŁŹ”±”ăC”ÄĆóÓŃÈŠÓĐșĂÓŃÂäÔÚÖ±ÏßÉÏʱŁŹÖ±Ïßœ«ÊÜÆäÓ°ÏìŁŹÇóÔÚ”ăCÏòÏÂÔ˶Ż”ÄčęłÌÖĐŁŹÖ±ÏßÊÜÆäÓ°Ïì”ÄʱŒäŁ»
Łš3Ł©ĆŚÎïÏßy=ax2+bx+cčęÔ”ăOșÍ”ăAŁŹÇÒ¶„”ăDÇĄșĂÎȘ”ăC”ÄșĂÓŃŁŹÁŹœÓODŁźEÎȘĄŃCÉÏÒ»”㣏”±ĄśDOEĂæ»ęŚîŽóʱŁŹÇó”ăE”ÄŚű±êŁŹŽËʱĄśDOE”ÄĂæ»ęÊǶàÉÙŁż
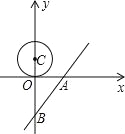
ĄŸŽđ°žĄżŁš1Ł©”㣚0ŁŹ0Ł©ĄąŁš0ŁŹ3Ł©ÎȘ”ăC”ÄșĂÓŃŁ»Łš2Ł©ÔÚ”ăCÏòÏÂÔ˶Ż”ÄčęłÌÖĐŁŹÖ±ÏßÊÜÆäÓ°Ïì”ÄʱŒäÎȘ6ĄÜtĄÜ16Ł»Łš3Ł©”±ĄśDOEĂæ»ęŚîŽóʱŁŹ”ăE”ÄŚű±êÎȘŁš©![]() ŁŹ
ŁŹ![]() Ł©ŁŹŽËʱĄśDOE”ÄĂæ»ęÊÇ
Ł©ŁŹŽËʱĄśDOE”ÄĂæ»ęÊÇ![]() Łź
Łź
ĄŸœâÎöĄż
ÊÔÌâ·ÖÎöŁșŁš1Ł©ÓÉĆóÓŃÈŠÒÔŒ°șĂÓєĶšÒ棏œáșÏÍŒĐÎŁŹŒŽżÉ”ĂłöœáÂÛŁ»Łš2Ł©ÉèÔČĐÄCÍùÏÂÔ˶ŻÁËtĂ룏Ôò”ăC”ÄŚű±êÎȘŁš0ŁŹ1.5©0.5tŁ©ŁŹžùŸĘșĂÓєĶšÒ棏œáșÏ”ăC”œÖ±Ïßl”ÄŸàÀëĐĄÓÚ”ÈÓÚ1.5ŁŹŒŽżÉ”ĂłöčŰÓÚʱŒät”ÄșŹŸű¶ÔÖ”·ûșĆ”ÄÒ»ÔȘÒ»ŽÎ·œłÌŁŹœâ·œłÌŒŽżÉ”ĂłöœáÂÛŁ»Łš3Ł©žùŸĘ¶țŽÎșŻÊę”ÄĐÔÖÊŐÒłöĆŚÎïÏߔĶԳÆÖᣏœáșÏșŻÊęÍŒÏóÒÔŒ°șĂÓєĶšÒćŐÒłö”ăD”ÄŚű±êŁ»ÁŹœÓODŁŹčę”ăCŚśCMĄÍODÓÚ”ăMŁŹŃÓł€MCœ»ÔČCÓÚ”ăEŁŹÁŹœÓEOĄąEDŁŹÍščęŽčŸ¶¶šÀíĄąœâÖ±œÇÈęœÇĐÎÇółöÏ߶ÎEM”Äł€ŁŹÔÙœáșÏÈęœÇĐΔÄĂæ»ęč«ÊœŒŽżÉÇółöSĄśDOE”ÄÖ”ŁŹÓÉ”ăCĄąM”ă”ÄŚű±êÀûÓĂŽę¶šÏ”Êę·šÇółöÖ±ÏßCM”ÄœâÎöÊœŁŹÉèłö”ăE”ÄŚű±êŁŹÔÙœáșÏÁœ”ăŒä”ÄŸàÀëč«ÊœŒŽżÉÇółö”ăE”ÄŚű±êŁŹŽËÌâ”ĂœâŁź
ÊÔÌâœâÎöŁșŁš1Ł©1.5©1.5=0ŁŹ1.5+1.5=3ŁŹ
Ąà”㣚0ŁŹ0Ł©ĄąŁš0ŁŹ3Ł©”œ”ăC”ÄŸàÀëÎȘ1.5ŁŹ
Ąà”㣚0ŁŹ0Ł©ĄąŁš0ŁŹ3Ł©ÎȘ”ăC”ÄșĂÓŃŁź
Łš2Ł©ÉèÔČĐÄCÍùÏÂÔ˶ŻÁËtĂ룏Ôò”ăC”ÄŚű±êÎȘŁš0ŁŹ1.5©0.5tŁ©ŁŹ
Ö±ÏßlŁșy=![]() x©4żÉ±äĐÎÎȘ4x©3y©12=0ŁŹ
x©4żÉ±äĐÎÎȘ4x©3y©12=0ŁŹ
”ăC”œÖ±Ïßl”ÄŸàÀëd= =|0.3t©3.3|ŁŹ
=|0.3t©3.3|ŁŹ
”±Ö±ÏßÊÜÔČCÓ°ÏìʱŁŹÓĐdĄÜ1.5ŁŹŒŽ|0.3t©3.3|ĄÜ1.5ŁŹ
œâ”ĂŁș6ĄÜtĄÜ16Łź
ĄàÔÚ”ăCÏòÏÂÔ˶Ż”ÄčęłÌÖĐŁŹÖ±ÏßÊÜÆäÓ°Ïì”ÄʱŒäÎȘ6ĄÜtĄÜ16Łź
Łš3Ł©Áîy=![]() x©4ÖĐy=0ŁŹÔò
x©4ÖĐy=0ŁŹÔò![]() x©4=0ŁŹ
x©4=0ŁŹ
œâ”ĂŁșx=3ŁŹŒŽ”ăA”ÄŚű±êÎȘŁš3ŁŹ0Ł©Łź
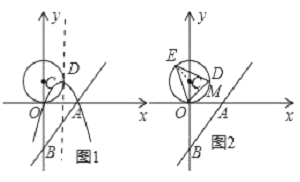
ÒÀŐŐÌâÒ⻳öÍŒĐÎŁŹÈçÍŒ1ËùÊŸŁź
ĄßĆŚÎïÏßy=ax2+bx+cčęÔ”ăOșÍ”ăAŁŹ”ăOŁš0ŁŹ0Ł©ŁŹ”ăAŁš3ŁŹ0Ł©ŁŹ
ĄàĆŚÎïÏߔĶԳÆÖáÎȘx=![]() =1.5ŁŹ
=1.5ŁŹ
Ąß”ăDÇĄșĂÎȘ”ăC”ÄșĂÓŃŁŹ
Ąà”ăD”ÄŚű±êÎȘŁš1.5ŁŹ1.5Ł©Łź
ÁŹœÓODŁŹčę”ăCŚśCMĄÍODÓÚ”ăMŁŹŃÓł€MCœ»ÔČCÓÚ”ăEŁŹÁŹœÓEOĄąEDŁŹŽËʱSĄśDOEŚîŽóŁŹÈçÍŒ2ËùÊŸŁź
ĄßODÊÇÔČC”ÄÏÒŁŹCMĄÍODŁŹ
Ąà”ăMÎȘÏ߶ÎOD”ÄÖД㣏
Ąà”ăM”ÄŚű±êÎȘŁš![]() ŁŹ
ŁŹ![]() Ł©ĄąOM=
Ł©ĄąOM=![]() =
=![]() ŁŹ
ŁŹ
ÔÚRtĄśCMOÖĐŁŹOM=![]() ŁŹCO=1.5=
ŁŹCO=1.5=![]() ŁŹ
ŁŹ
ĄàCM=![]() =
=![]() Łź
Łź
ĄßCE=1.5=![]() ŁŹEM=EC+CMŁŹ
ŁŹEM=EC+CMŁŹ
ĄàEM=![]() ŁŹ
ŁŹ
ŽËʱSĄśDOE=![]() ODEM=OMEM=
ODEM=OMEM=![]() ĄÁ
ĄÁ![]() =
=![]() Łź
Łź
ÉèÖ±ÏßCM”ÄœâÎöÊœÎȘy=mx+nŁŹ
Ąß”ăC”ÄŚű±êÎȘŁš0ŁŹ1.5Ł©Ąą”ăM”ÄŚű±êÎȘŁš![]() ŁŹ
ŁŹ![]() Ł©ŒŽŁš0.75ŁŹ0.75Ł©ŁŹ
Ł©ŒŽŁš0.75ŁŹ0.75Ł©ŁŹ
Ąà![]() ŁŹœâ”ĂŁș
ŁŹœâ”ĂŁș![]() ŁŹ
ŁŹ
ĄàÖ±ÏßCM”ÄœâÎöÊœÎȘy=©x+1.5Łź
Éè”ăE”ÄŚű±êÎȘŁšxŁŹ©x+1.5Ł©ŁšxŁŒ0Ł©ŁŹ
ĄßEC=![]() =1.5ŁŹ
=1.5ŁŹ
Ąàx=©![]() ŁŹ»òx=
ŁŹ»òx=![]() ŁšÉáÈ„Ł©ŁŹ
ŁšÉáÈ„Ł©ŁŹ
Ąà”ăE”ÄŚű±êÎȘŁš©![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź
čÊ”±ĄśDOEĂæ»ęŚîŽóʱŁŹ”ăE”ÄŚű±êÎȘŁš©![]() ŁŹ
ŁŹ![]() Ł©ŁŹŽËʱĄśDOE”ÄĂæ»ęÊÇ
Ł©ŁŹŽËʱĄśDOE”ÄĂæ»ęÊÇ![]() Łź
Łź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłÊÖ»úŚšÂô”êÏúÊÛAŁŹBÁœÖÖĐÍșĆ”ÄÊÖ»úŁŹÈç±íÊÇœüÁœÖÜ”ÄÏúÊÛÇéżöŁș
ÏúÊÛʱ¶Î | ÏúÊÛÊęÁż | ÏúÊÛÀûÈó | |
AĐÍ | BĐÍ | ||
”ÚÒ»ÖÜ | 3Ìš | 5Ìš | 1800ÔȘ |
”Ú¶țÖÜ | 4Ìš | 10Ìš | 3000ÔȘ |
Łš1Ł©ÇóĂżÌšAĐÍÊÖ»úșÍBĐÍÊÖ»ú”ÄÏúÊÛÀûÈóŁ»
Łš2Ł©žĂÊÖ»úŚšÂô”êŒÆ»źÒ»ŽÎčșœűÁœÖÖĐÍșĆ”ÄÊÖ»účČ100ÌšŁŹÆäÖĐAĐÍșĆÊÖ»ú”Äœű»őÁżČ»łŹčęBĐÍșĆÊÖ»úœű»őÁż”Ä2±¶ŁźÉèčșœűAĐÍșĆÊÖ»úxÌšŁŹŐâ100ÌšÊÖ»ú”ÄÏúÊÛŚÜÀûÈóÎȘyÔȘŁź
ąÙÇóyčŰÓÚx”ÄșŻÊę±íŽïÊœŁ»
ąÚžĂÉÌ”êčșœűAĐÍșĆșÍBĐÍșĆÊÖ»úžś¶àÉÙÌšŁŹČĆÄÜÊčÏúÊÛŚÜÀûÈóŚîŽóŁż
Łš3Ł©Ê”ŒÊœű»őʱŁŹł§ŒÒ¶ÔAĐÍșĆÊÖ»ú”Äłöł§ŒÛÌážßaŁš0ŁŒaŁŒ100Ł©ÔȘŁŹ¶ÔBĐÍșĆÊÖ»ú”Äłöł§ŒÛÏÂœ”aŁš0ŁŒaŁŒ100Ł©ÔȘŁŹÇÒÏȚ¶šžĂÊÖ»úŚšÂô”êÖÁÉÙčșœűAĐÍșĆÊÖ»ú20ÌšŁźÈôžĂÊÖ»úŚšÂô”ê±ŁłÖÁœÖÖÊÖ»ú”ÄÊÛŒÛČ»±äŁŹÇëžùŸĘÒÔÉÏĐĆÏąŒ°Łš2Ł©ÖĐÌőŒțŁŹÉèŒÆłöÊčŐâ100ÌšÊÖ»úÏúÊÛŚÜÀûÈóŚîŽó”Äœű»ő·œ°žŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘaÊÇŚîŽó”ÄžșŐûÊ꣏bÊÇŸű¶ÔÖ”ŚîĐĄ”ÄÊ꣏cÊÇŚîĐĄ”ÄŐęŐûÊ꣏Ôò2a+3b©4c”ÈÓÚŁš Ł©
A. 2 B. ©2 C. 0 D. ©6
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŒÆËăŁș
Łš1Ł©Łš©8Ł©©Łš©5Ł©+Łš©2Ł©
Łš2Ł©©12ĄÁ2+Łš©2Ł©2ĄÂ4©Łš©3Ł©
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎÒĂÇŃ§Ï°ÁËčŽčɶšÀíș󣏶ŒÖȘ”ÀĄ°čŽÈꥹčÉËÄĄąÏÒÎ楱Łź
čÛČìŁș3Ąą4Ąą5Ł»5Ąą12Ąą13Ł»7Ąą24Ąą25Ł»9Ąą40Ąą41Ł»ĄŁŹ·ąÏÖŐâĐ©čŽčÉÊę”Ä莶ŒÊÇÆæÊ꣏ÇÒŽÓ3ÆđŸÍĂ»ÓĐŒä¶Ïč꣟
Łš1Ł©ÇëÄăžùŸĘÉÏÊö”ÄčæÂÉĐŽłöÏÂÁœŚéčŽčÉÊęŁș11ĄąĄĄĄĄĄą Ł» 13ĄąĄĄĄąĄĄŁ»
Łš2Ł©Èô”ÚÒ»žöÊęÓĂŚÖÄžaŁšaÎȘÆæÊ꣏ÇÒaĄĘ3Ł©±íÊŸŁŹÄÇĂŽșóÁœžöÊęÓĂșŹa”ÄŽúÊęÊœ·Ö±đ±íÊŸÎȘĄĄĄĄșÍĄĄĄĄŁŹÇëÓĂËùѧÖȘÊ¶Ë”ĂśËüĂÇÊÇÒ»ŚéčŽčÉÊ꣟
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłĐĄŚé6Ăû͏ѧ”ÄÌćÓęłÉŒšŁšÂú·Ö40·ÖŁ©·Ö±đÎȘŁș36ŁŹ40ŁŹ38ŁŹ38ŁŹ32ŁŹ35ŁŹŐâŚéÊęŸĘ”ÄÖĐλÊęÊÇ·ÖŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒËùÊŸŁŹÊÇÒ»ÁĐÓĂÈôžÉžù»đČń°ô°ÚłÉ”ÄÓÉŐę·œĐÎŚéłÉ”ÄÍŒ°žŁź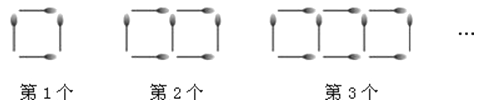
Łš1Ł©ÍêłÉϱí”ÄÌîżŐŁș
Őę·œĐΞöÊę | 1 | 2 | 3 | 4 | 5 | 6 | n |
»đČń°ôžùÊę | 4 | 7 | 10 | 13 |
Łš2Ł©ÄłÍŹŃ§ÓĂÈôžÉžù»đČń°ô°ŽÈçÉÏÍŒÁДķœÊœ°ÚÍŒ°žŁŹ°ÚÍêÁË”Ú1žöșóŁŹ°Ú”Ú2žöŁŹœÓŚĆ°Ú”Ú3žöŁŹ”Ú4žöŁŹĄŁŹ”±Ëû°ÚÍê”ÚnžöÍŒ°žÊ±ÊŁÏÂÁË20žù»đČń°ôŁŹÒȘžŐșĂ°ÚÍê”Ún+1žöÍŒ°ž»čČî2žùŁźÎÊŚîșó°Ú”ÄÍŒ°žÊǔڌžžöÍŒ°žŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŒÆËăŁș
Łš1Ł©8©Łš©2Ł©©Łš+3Ł©+Łš©1Ł©
Łš2Ł©Łš©12Ł©ĄÂŁš+4Ł©©Łš©2Ł©ĄÁŁš©3Ł©
Łš3Ł©![]()
Łš4Ł©![]() Łź
Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘĄśABCĄŐĄśDEFŁŹÈôAB=5ŁŹBC=6ŁŹAC=8ŁŹÔòĄśDEF”ÄÖÜł€ÊÇ_________.
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com