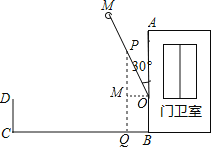
【题目】如图，是某小区入口抽象成的平面示意图，已知入口BC宽4米，栏杆支点O与地面BC的距离为0.8米，当栏杆OM升起到与门卫室外墙AB的夹角成30°时，一辆宽2.4米，高1.6米的轿车能否从该入口的正中间位置进入该小区？若能，请通过计算说明；若不能，请说明理由．（参考数据：
1.7）
【答案】轿车能安全通过，理由见解析．
【解析】
直接在BC上取点Q，使BQ＝0.8m，过Q作QP⊥BC交MO于点P，过O作OM⊥OQ于点M，分别得出PM，PQ的长进而得出答案．
解：轿车能安全通过．
理由：如图所示：当轿车从该入口的正中间位置进入该小区时，
车与OB的距离为：4.0÷2﹣2.4÷2＝0.8（m），
在BC上取点Q，使BQ＝0.8m，过Q作QP⊥BC交MO于点P，
过O作OM⊥OQ于点M，
则MQ＝OB＝0.8m，OM＝BQ＝0.8m，
在Rt△OPM中，
∵tan60°＝
，
∴PM＝OMtan60°＝0.8×
＝1.36（m），
∴PQ＝PM+MQ＝2.16m＞1.6m，
∴轿车能安全通过．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c的图象如图所示，下列结论：①b＜2a；②a+2c﹣b＞0；③b＞a＞c；④b2+2ac＜3ab．其中正确结论的个数是（ ）
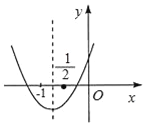
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解本校学生每周参加课外辅导班的情况，随机调査了部分学生一周内参加课外辅导班的学科数，并将调查结果绘制成如图1、图2所示的两幅不完整统计图（其中A：0个学科，B：1个学科，C：2个学科，D：3个学科，E：4个学科或以上），请根据统计图中的信息，解答下列问题：
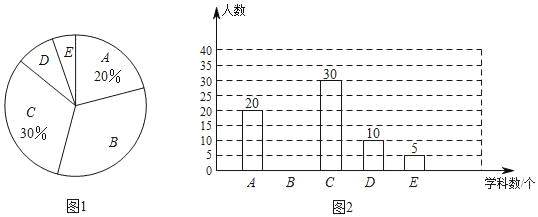
（1）请将图2的统计图补充完整；
（2）根据本次调查的数据，每周参加课外辅导班的学科数的众数是 个学科；
（3）若该校共有2000名学生，根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科（含3个学科）以上的学生共有 人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1是一台实物投影仪，图2是它的示意图，折线O﹣A﹣B﹣C表示支架，支架的一部分O﹣A﹣B是固定的，另一部分BC是可旋转的，线段CD表示投影探头，OM表示水平桌面，AO⊥OM，垂足为点O，且AO＝7cm，∠BAO＝160°，BC∥OM，CD＝8cm．
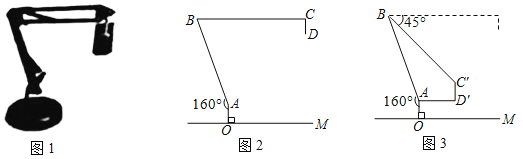
将图2中的BC绕点B向下旋转45°，使得BCD落在BC′D′的位置（如图3所示），此时C′D′⊥OM，AD′∥OM，AD′＝16cm，求点B到水平桌面OM的距离，（参考数据：sin70°≈0.94，cos70°≈0.34，cot70°≈0.36，结果精确到1cm）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'=1，则A'D等于（ ）
A. 2 B. 3 C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
为双曲线
上的一点，连接
并延长与双曲线在第三象限交于点
，
为
轴正半轴上一点，连接
并延长与双曲线交于点
，连接
、
，已知
的面积为6，则点的坐标为______．
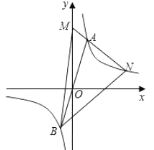
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=3+
,∠B=45°，∠C=105°，点 D、E、F分别在AC、BC、AB上，且四边形ADEF为菱形，若点P是AE上一个动点，则PF+PB的最小值为___________ 。
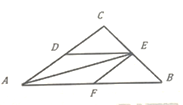
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知方格纸中的每个小方格都是相同的正方形（边长为1），方格纸上有一个角∠AOB，A，O，B均为格点，请回答问题并只用无刻度直尺和铅笔，完成下列作图并简要说明画法：
（1）OA＝_____；
（2）作出∠AOB的平分线并在其上标出一个点Q，使OQ＝
．
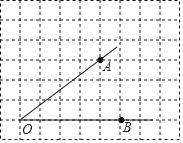
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
