【题目】如图，正方形
的边长为10，
，
，连接
，则线段的长为（ ）
A.
B.
C.
D.
【答案】B
【解析】
延长DH交AG于点E，利用SSS证出△AGB≌△CHD，然后利用ASA证出△ADE≌△DCH，根据全等三角形的性质求出EG、HE和∠HEG，最后利用勾股定理即可求出HG．
解：延长DH交AG于点E
∵四边形ABCD为正方形
∴AD=DC=BA=10，∠ADC=∠BAD=90°
在△AGB和△CHD中
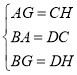
∴△AGB≌△CHD
∴∠BAG=∠DCH
∵∠BAG＋∠DAE=90°
∴∠DCH＋∠DAE=90°
∴CH2＋DH2=82＋62=100= DC2
∴△CHD为直角三角形，∠CHD=90°
∴∠DCH＋∠CDH=90°
∴∠DAE=∠CDH，
∵∠CDH＋∠ADE=90°
∴∠ADE=∠DCH
在△ADE和△DCH中
∴△ADE≌△DCH
∴AE=DH=6，DE=CH=8，∠AED=∠DHC=90°
∴EG=AG－AE=2，HE= DE－DH=2，∠GEH=180°－∠AED=90°
在Rt△GEH中，GH=
故选B．
教材全解字词句篇系列答案科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图象开口向上，图象经过点（－1，2）和（1，0），且与y
轴相交于负半轴。给出四个结论：①
；②
；③
；④
，其中正确结论的序
号是___________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，两线相交于F点．
（1）若∠BAC=60°，∠C=70°，求∠AFB的大小；
（2）若D是BC的中点，∠ABE=30°，求证：△ABC是等边三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=3x与双曲线y=
（k≠0，且x＞0）交于点A，点A的横坐标是1．
（1）求点A的坐标及双曲线的解析式；
（2）点B是双曲线上一点，且点B的纵坐标是1，连接OB，AB，求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于
的一元二次方程x2-(k+2)x+k-1=0
（1）若方程的一个根为 -1，求
的值和方程的另一个根；
（2）求证：不论取何值，该方程都有两个不相等的实数根．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高3米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有27米的距离（B，F，C在一条直线上）．
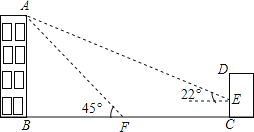
（1）求办公楼AB的高度；
（2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．
（参考数据：sin22°≈
，cos22°≈
，tan22°≈
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列结论中，错误的有( )
①在Rt△ABC中，已知两边长分别为3和4，则第三边的长为5；
②△ABC的三边长分别为AB，BC，AC，若
+
=
，则∠A=90°；
③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；
④若三角形的三边长之比为3：4：5，则该三角形是直角三角形．
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
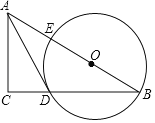
【题目】如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知∠CAD=∠B．
（1）求证：AD是⊙O的切线．
（2）若BC=8，tanB=
，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与
轴，
轴分别交于
，
两点，若将直线
向右平移
个单位得到直线
，与轴，轴分别交于
，
两点．
（1）求点的坐标；
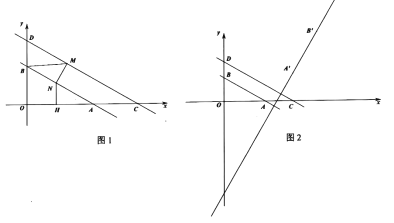
（2）如图1，若点
是直线上一动点，且
，
轴，连接
，求
的最小值及此时点
的坐标；
（3）如图2，将线段
绕点顺时针旋转
，得到线段
，延长线段得到直线
，线段在直线上移动，当以点、
、
构成的三角形是等腰三角形时，直接写出点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com