
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O的半径.
,求⊙O的半径.
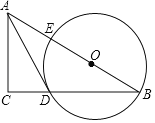
【答案】(1)证明见解析;(2)r=![]() .
.
【解析】(1)连接OD,由OD=OB,利用等边对等角得到一对角相等,再由已知角相等,等量代换得到∠1=∠3,求出∠4为90°,即可得证;
(2)设圆的半径为r,利用锐角三角函数定义求出AB的长,再利用勾股定理列出关于r的方程,求出方程的解即可得到结果.
详(1)证明:连接OD,
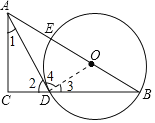
∵OB=OD,
∴∠3=∠B,
∵∠B=∠1,
∴∠1=∠3,
在Rt△ACD中,∠1+∠2=90°,
∴∠4=180°-(∠2+∠3)=90°,
∴OD⊥AD,
则AD为圆O的切线;
(2)设圆O的半径为r,
在Rt△ABC中,AC=BCtanB=4,
根据勾股定理得:AB=![]() ,
,
∴OA=4![]() -r,
-r,
在Rt△ACD中,tan∠1=tanB=![]() ,
,
∴CD=ACtan∠1=2,
根据勾股定理得:AD2=AC2+CD2=16+4=20,
在Rt△ADO中,OA2=OD2+AD2,即(4![]() -r)2=r2+20,
-r)2=r2+20,
解得:r=![]() .
.


科目:初中数学 来源: 题型:
【题目】直线y=kx+3和x轴、y轴的交点分别为B、C,∠OBC=30°,点A的坐标是(![]() ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
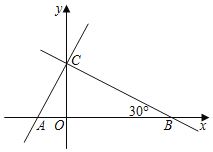
(1)求点B的坐标及k的值;
(2)求证:AC⊥BC;
(3)点M为直线BC上一点(与点B不重合),设点M的横坐标为x,△ABM的面积为S.
①求S与x的函数关系式;
②当S=6![]() 时,求点M的坐标.
时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九年(1)班的2名男生1名女生(男生用A1表示,女生用B1表示)和九年(2)班的1名男生1名女生(男生用A2表示,女生用B2表示)共5人中随机选出2名主持人.
(1)用树状图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
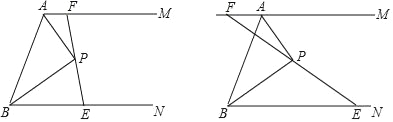
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】半期考试来临,元元到文具店购买考试用的铅笔,签字笔和钢笔,其中铅笔每支8元,签字笔每支l0元,钢笔每支20元,若他一共用了122元,那么他最多能买钢笔_______支.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com