
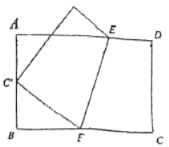
【题目】如图,将矩形![]() 沿
沿![]() 折叠,使顶点
折叠,使顶点![]() 恰好落在
恰好落在![]() 边的中点
边的中点![]() 处,若
处,若![]() ,
,![]() ,则
,则![]() 的长为___________.
的长为___________.
【答案】6
【解析】
先根据勾股定理求出BF,再根据△AMC′∽△BC′F求出AM、MC′、MD′,再证明△MAC′≌△MD′E,可得EM=MC′即可解决问题.
解:根据折叠的性质可知,FC=FC′,∠C=∠FC′M=90°,

设BF=x,则FC=FC′=9-x,
∵BF2+BC′2=FC′2,
∴x2+32=(9-x)2,
解得:x=4,
∵∠FC′M=90°,
∴∠AC′M+∠BC′F=90°,
又∵∠BFC′+BC′F=90°,
∴∠AC′M=∠BFC′
∵∠A=∠B=90°
∴△AMC′∽△BC′F
∴![]() ,
,
∵BC′=AC′=3,
∴AM=![]() ,
,
∴MC′=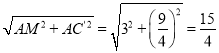 ,
,
∴D′M=6-![]() =
=![]() ,
,
∴AM=MD′,
∵∠A=∠D′=90°,∠AMC′=∠EMD′,
∴△MAC′≌△MD′E,
∴EM=MC′=![]() ,
,
∴AE=AM+EM=![]() ,
,
故答案为6.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
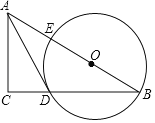
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,若将直线
两点,若将直线![]() 向右平移
向右平移![]() 个单位得到直线
个单位得到直线![]() ,
,![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求点![]() 的坐标;
的坐标;
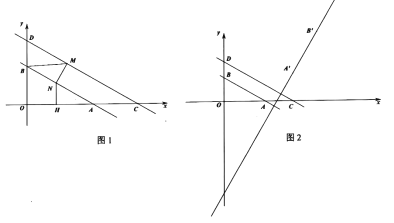
(2)如图1,若点![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() ,
,![]() 轴,连接
轴,连接![]() ,求
,求![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
(3)如图2,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,延长线段
,延长线段![]() 得到直线
得到直线![]() ,线段
,线段![]() 在直线
在直线![]() 上移动,当以点
上移动,当以点![]() 、
、![]() 、
、![]() 构成的三角形是等腰三角形时,直接写出点
构成的三角形是等腰三角形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
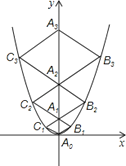
【题目】二次函数y=![]() 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
=60°,菱形An﹣1BnAnCn的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
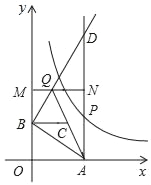
【题目】如图所示,已知:![]() (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2![]() ,此时P点的坐标为( )
,此时P点的坐标为( )
A. (3,2) B. (![]() ,3
,3![]() ) C. (
) C. (![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.

(1)如图1,![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(2)如图2,若![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,请猜想
,请猜想![]() 三者之间的数量关系,并证明你的结论;
三者之间的数量关系,并证明你的结论;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com