
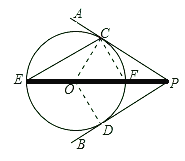
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题(1)连接OC,作OD⊥PB于D点.证明OD=OC即可.根据角的平分线性质易证;
(2)设PO交⊙O于F,连接CF.根据勾股定理得PO=5,则PE=8.证明△PCF∽△PEC,得CF:CE=PC:PE=1:2.根据勾股定理求解CE.
试题解析:(1)证明:连接OC,作OD⊥PB于D点.
∵⊙O与PA相切于点C, ∴OC⊥PA.
(2)解:设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.
∵⊙O与PA相切于点C, ∴∠PCF=∠E.
又∵∠CPF=∠EPC, ∴△PCF∽△PEC,
∴CF:CE=PC:PE=4:8=1:2.
∵EF是直径, ∴∠ECF=90°.
设CF=x,则EC=2x.
则x2+(2x)2=62, 解得x=![]() .
.
则EC=2x=![]() .
.


科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校园绿化工程,已知甲、乙两队单独完成这项工程所需时间比是2:3,且两队合作6天可以完成.
(1)求甲、乙两队单独完成此工程分别需要多少天?
(2)甲队工作一天需付报酬3500元,乙队工作一天需付报酬2000元,学校需要在9天内完成绿化工作,学校该如何安排甲、乙两队工作时间,才能使得所付报酬最少?最少报酬是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
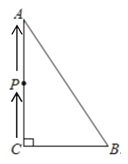
【题目】如图,△ABC中,![]() ,
,![]() ,
,![]() ,若点P从点C出发,以每秒1cm的速度沿折线C→A→B→C运动(回到C点后点P停止运动),设运动时间为t秒(
,若点P从点C出发,以每秒1cm的速度沿折线C→A→B→C运动(回到C点后点P停止运动),设运动时间为t秒(![]() ).
).
(1)若点P点AB边上,且满足![]() 时,求出此时t的值;
时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求出此时t的值;
(3)在运动过程中,当△BCP为等腰三角形时,直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲同学从某小区出发步行前往学校.若干分钟后乙同学从学校出发骑自行车前往这个小区,他在小区停留一段时间后,以另一速度(千米![]() 分)沿原路返回.返回途中遇到了甲同学,用自行车搭载上甲同学减速返回学校,他们到达学校的时间比甲同学一直步行到学校的时间提前了
分)沿原路返回.返回途中遇到了甲同学,用自行车搭载上甲同学减速返回学校,他们到达学校的时间比甲同学一直步行到学校的时间提前了![]() 分钟.两人与学校的距离
分钟.两人与学校的距离![]() (千米)和乙同学从学校出发后所用的时间
(千米)和乙同学从学校出发后所用的时间![]() (分)之间的关系如图.
(分)之间的关系如图.
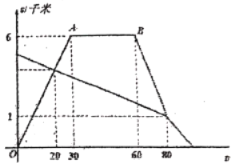
(1)两人第一次相遇时,距学校____________千米,![]() ____________(直接写出答案);
____________(直接写出答案);
(2)甲同学从小区出发多久后,乙同学从学校出发?
(3)求乙同学用自行车搭载上甲同学一起到学校的行进速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
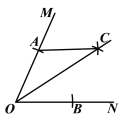
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A. 5 B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com