
【题目】由甲、乙两个工程队承包某校园绿化工程,已知甲、乙两队单独完成这项工程所需时间比是2:3,且两队合作6天可以完成.
(1)求甲、乙两队单独完成此工程分别需要多少天?
(2)甲队工作一天需付报酬3500元,乙队工作一天需付报酬2000元,学校需要在9天内完成绿化工作,学校该如何安排甲、乙两队工作时间,才能使得所付报酬最少?最少报酬是多少?
【答案】(1)甲、乙两队单独完成此工程分别需要10天、15天;(2)甲乙两队合作4天,乙队单独干5天,学校付报酬最低,最低32000元.
【解析】
(1)设甲队单独完成此工程需x天,则可表示出乙队单独完成此工程需![]() 天,利用工作量为1列方程
天,利用工作量为1列方程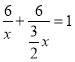 ,再解方程、检验,然后计算
,再解方程、检验,然后计算![]() 即可;
即可;
(2)设甲队干了m天,乙队干了n天,则![]() ,通过代换得到报酬的一次函数关系式,利用不等式的关系求解即可.
,通过代换得到报酬的一次函数关系式,利用不等式的关系求解即可.
设甲队单独完成此工程需x天,则乙队单独完成此工程需![]() 天,
天,
根据题意得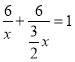 ,
,
解得x=10,
经检验x=10是原方程的解,
当x=10时,![]() =15,
=15,
答:甲、乙两队单独完成此工程分别需要10天、15天,
故答案为:10;15;
(2)设甲、乙两队合作干了m天,然后乙队又单独干了n天,则
![]() ,
,![]() ,
,
解得m=6-![]() ,
,
代入不等式得,6-![]() +n
+n![]() 9,
9,
解得:n![]() 5,
5,
学校需要付的报酬为:
(3500+2000)m+2000n=5500m+2000n=33000-2200n+2000n=33000-200n,
∵-200<0,n值越大,学校付的报酬越少,
∴n=5时,原式=33000-1000=32000(元),
此时m=4,
答:甲乙合作4天,然后乙队单独干5天,学校付的报酬最低,最低32000元,
故答案为:甲乙两队合作4天,乙队单独干5天,学校付报酬最低,最低32000元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若![]() +
+![]() =
=![]() ,则∠A=90°;
,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,若将直线
两点,若将直线![]() 向右平移
向右平移![]() 个单位得到直线
个单位得到直线![]() ,
,![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求点![]() 的坐标;
的坐标;
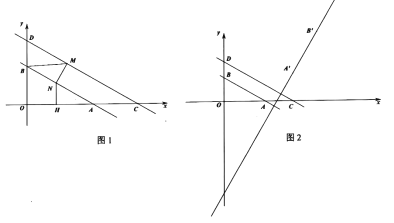
(2)如图1,若点![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() ,
,![]() 轴,连接
轴,连接![]() ,求
,求![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
(3)如图2,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,延长线段
,延长线段![]() 得到直线
得到直线![]() ,线段
,线段![]() 在直线
在直线![]() 上移动,当以点
上移动,当以点![]() 、
、![]() 、
、![]() 构成的三角形是等腰三角形时,直接写出点
构成的三角形是等腰三角形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
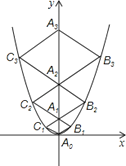
【题目】二次函数y=![]() 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
=60°,菱形An﹣1BnAnCn的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
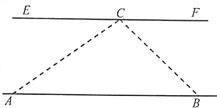
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com