
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,若将直线
两点,若将直线![]() 向右平移
向右平移![]() 个单位得到直线
个单位得到直线![]() ,
,![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求点![]() 的坐标;
的坐标;
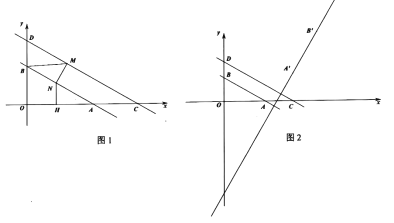
(2)如图1,若点![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() ,
,![]() 轴,连接
轴,连接![]() ,求
,求![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
(3)如图2,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,延长线段
,延长线段![]() 得到直线
得到直线![]() ,线段
,线段![]() 在直线
在直线![]() 上移动,当以点
上移动,当以点![]() 、
、![]() 、
、![]() 构成的三角形是等腰三角形时,直接写出点
构成的三角形是等腰三角形时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)D(0,5);(2)![]() +
+![]() ;N(
;N(![]() ,
,![]() );(3)A'(
);(3)A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );A'(
);A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );A'(5
);A'(5![]() -
-![]() ,-
,-![]() );
);
【解析】
(1)求出直线L2:y=-![]() x+5即可求出D;
x+5即可求出D;
(2)求出两直线间距离MN=![]() ,作B点关于L2的对称点B',与L2的交点为F,过点F作FH⊥x轴,交于L1于N,过点N作MN⊥L2,则BM+MN+NH的最小值即为
,作B点关于L2的对称点B',与L2的交点为F,过点F作FH⊥x轴,交于L1于N,过点N作MN⊥L2,则BM+MN+NH的最小值即为![]() +FH;过点B作BG⊥FH,在Rt△BGF中,∠FBG=60°,BF=
+FH;过点B作BG⊥FH,在Rt△BGF中,∠FBG=60°,BF=![]() ,求出F(
,求出F(![]() );在Rt△BNG中,∠GBN=30°,BG=
);在Rt△BNG中,∠GBN=30°,BG=![]() ,求出N(
,求出N(![]() ,
,![]() ),则可求FH=
),则可求FH=![]() ,即可德奥BM+MN+NH的最小值
,即可德奥BM+MN+NH的最小值![]() +
+![]() ;
;
(3)由已知可知,AC⊥A'C,AC=A'C,求得A'(5![]() ,2
,2![]() ),再由直线L1与直线L3垂直,可求直线L3:y=
),再由直线L1与直线L3垂直,可求直线L3:y=![]() x+2
x+2![]() -15,设A'(m,
-15,设A'(m,![]() m+2
m+2![]() -15),则B'(m+3,
-15),则B'(m+3,![]() m+5
m+5![]() -15),
-15),
①当A'B'=A'C时,A'C=6,所以36=(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2;②当A'B'=B'C时,B'C=6,所以36=(m+35
15)2;②当A'B'=B'C时,B'C=6,所以36=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2,③当A'C=B'C时,(m5
15)2,③当A'C=B'C时,(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2=(m+35
15)2=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2span>,分别求出m即可.
15)2span>,分别求出m即可.
(1)由已知可得A(3![]() ,0),B(0,3),
,0),B(0,3),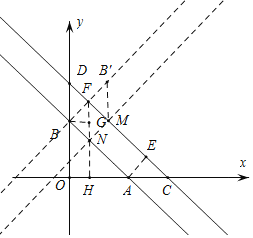
∵将直线l1向右平移2![]() 个单位得到直线L2,
个单位得到直线L2,
∴C(5![]() ,0),
,0),
∴直线L2:y=![]() x+5,
x+5,
∴D(0,5);
(2)过点A作AE⊥L2,
∵AC=2![]() ,∠DCA=30°,
,∠DCA=30°,
∴AE=![]() ,
,
∴MN=![]() ,
,
∴BM+MN+NH的最小值即为BM+![]() +NH的最小值,
+NH的最小值,
作B点关于L2的对称点B',与L2的交点为F,过点F作FH⊥x轴,交于L1于N,过点N作MN⊥L2,
则BM+MN+NH的最小值即为![]() +FH;
+FH;
由作图可得,四边形FNMB'是平行四边形,
∴B'M=FN,
∵B与B'关于L2对称,
∴BM=B'M,
∴BM=FN,
在Rt△BDF中,BF=![]() ,BD=2,
,BD=2,
∴∠DBF=30°,
过点B作BG⊥FH,
在Rt△BGF中,∠FBG=60°,BF=![]() ,
,
∴GB=![]() ,FG=
,FG=![]() ,
,
∴F(![]() ,
,![]() ),
),
在Rt△BNG中,∠GBN=30°,BG=![]() ,
,
∴GN=![]() ,
,
∴N(![]() ,
,![]() ),
),
∴FH=![]() ,
,
∴BM+MN+NH的最小值![]() +
+![]() ;
;
(3)由已知可知,AC⊥A'C,AC=A'C,
∴A'(5![]() ,2
,2![]() ),
),
∵直线L1与直线L3垂直,
∴直线L3:y=![]() x+2
x+2![]() -15,
-15,
∵A(3![]() ,0),B(0,3),
,0),B(0,3),
∴AB=6,
设A'(m,![]() m+2
m+2![]() -15),则B'(m+3,
-15),则B'(m+3,![]() m+5
m+5![]() -15),
-15),
①当A'B'=A'C时,A'C=6,
∴36=(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2
15)2
∴m=![]() 或m=
或m=![]() ,
,
∴A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
②当A'B'=B'C时,B'C=6,
∴36=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2,
15)2,
∴m=![]() 或m=
或m=![]() ;
;
∴A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
③当A'C=B'C时,
(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2=(m+35
15)2=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2,
15)2,
∴m=5![]() -
-![]() ;
;
∴A'(5![]() -
-![]() ,-
,-![]() );
);
综上所述A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
,A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
;A'(5![]() -
-![]() ,-
,-![]() );
);


科目:初中数学 来源: 题型:
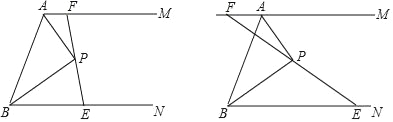
【题目】如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】半期考试来临,元元到文具店购买考试用的铅笔,签字笔和钢笔,其中铅笔每支8元,签字笔每支l0元,钢笔每支20元,若他一共用了122元,那么他最多能买钢笔_______支.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,BD为AC的中线,过点C作
,BD为AC的中线,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校园绿化工程,已知甲、乙两队单独完成这项工程所需时间比是2:3,且两队合作6天可以完成.
(1)求甲、乙两队单独完成此工程分别需要多少天?
(2)甲队工作一天需付报酬3500元,乙队工作一天需付报酬2000元,学校需要在9天内完成绿化工作,学校该如何安排甲、乙两队工作时间,才能使得所付报酬最少?最少报酬是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com