
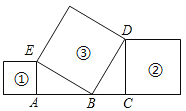
【题目】已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的边长分别为![]() 和
和![]() ,则正方形③的边长为( )
,则正方形③的边长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据正方形的性质就可以得出∠EAB=∠EBD=∠BCD=90°,BE=BD,∠AEB=∠CBD,就可以得出△ABE≌△CDB,得出AE=BC,AB=CD,由勾股定理就可以得出BE的值,进而得出结论.
∵四边形①、②、③都是正方形,
∴∠EAB=∠EBD=∠BCD=90°,BE=BD,
∴∠AEB+∠ABE=90°,∠ABE+∠DBC=90°,
∴∠AEB=∠CBD.
在△ABE和△CDB中,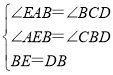 ,
,
∴△ABE≌△CDB(AAS),
∴AE=BC=9cm,AB=CD=12cm.
∴AE2=81,AB2=144.
在Rt△ABE中,由勾股定理,得
BE2=AE2+AB2=81+144=225,
∴BE=15.
故选:D.


科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
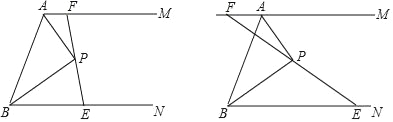
【题目】如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行
河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,
沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
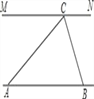
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】半期考试来临,元元到文具店购买考试用的铅笔,签字笔和钢笔,其中铅笔每支8元,签字笔每支l0元,钢笔每支20元,若他一共用了122元,那么他最多能买钢笔_______支.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校园绿化工程,已知甲、乙两队单独完成这项工程所需时间比是2:3,且两队合作6天可以完成.
(1)求甲、乙两队单独完成此工程分别需要多少天?
(2)甲队工作一天需付报酬3500元,乙队工作一天需付报酬2000元,学校需要在9天内完成绿化工作,学校该如何安排甲、乙两队工作时间,才能使得所付报酬最少?最少报酬是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com