练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某玩具店进了一排黑白塑料球，共5箱，每箱的规格、数量都相同，其中每箱中装有黑白两种颜色的塑料球共3000个，为了估计每箱中两种颜色球的个数，随机抽查了一箱，将箱子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回箱子中，多次重复上述过程后，发现摸到黑球的概率在0.8附近波动，则此可以估计这批塑料球中黑球的总个数，请将黑球总个数用科学记数法表示约为________个．

    【答案】1.2×104

    【解析】

    因为摸到黑球的频率在0.8附近波动，所以摸出黑球的概率为0.8，再设出黑球的个数，根据概率公式列方程解答即可．

    设黑球的个数为x．

    ∵黑球的频率在0.8附近波动，∴摸出黑球的概率为0.8，即0.8，解得：x＝2400．

    所以可以估计黑球的个数为2400×5＝12000＝1.2×104个．

    故答案为：1.2×104．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明：当销售价为2900元时,平均每天能售出8部；而当销售价每降低50元时,平均每天就能多售出4部.

    （1）当售价为2800元时,这种手机平均每天的销售利润达到多少元?

    （2）若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式．

    （3）商场要想获得最大利润,每部手机的售价应订为为多少元？此时的最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的一元二次方程x2-(k+2)x+k-1=0

    （1）若方程的一个根为 -1，求的值和方程的另一个根；

    （2）求证：不论取何值，该方程都有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列结论中，错误的有( )

    ①在Rt△ABC中，已知两边长分别为3和4，则第三边的长为5；

    ②△ABC的三边长分别为AB，BC，AC，若+=，则∠A=90°；

    ③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；

    ④若三角形的三边长之比为3：4：5，则该三角形是直角三角形．

    A. 0个 B. 1个 C. 2个 D. 3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个盒子里有完全相同的三个小球，球上分别标上数字－1、1、2.随机摸出一个小球(不放回)，其数字记为p，再随机摸出另一个小球，其数字记为q，则p，q使关于x的方程x2＋px＋q＝0有实数根的概率是(　　)

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

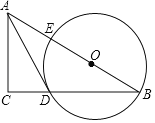
    【题目】如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知∠CAD=∠B．

    （1）求证：AD是⊙O的切线．

    （2）若BC=8，tanB=，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

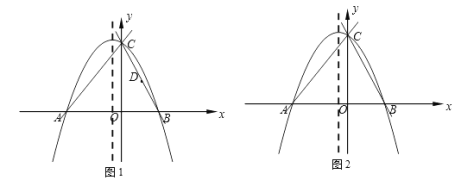
    【题目】已知，抛物线y=ax+bx+4与x轴交于点A（-3，0）和B（2，0），与y轴交于点C．

    （1）求抛物线的解析式；

    （2）如图1，若点D为CB的中点，将线段DB绕点D旋转，点B的对应点为点G，当点G恰好落在抛物线的对称轴上时，求点G的坐标；

    （3）如图2，若点D为直线BC或直线AC上的一点，E为x轴上一动点，抛物线y=ax+bx+4对称轴上是否存在点F，使以B，D，F，E为顶点的四边形为菱形？若存在，请求出点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正方形①、②在直线上，正方形③如图放置，若正方形①、②的边长分别为和，则正方形③的边长为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O在∠APB的平分线上，⊙O与PA相切于点C．

    （1）求证：直线PB与⊙O相切；

    （2）PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．

    查看答案和解析>>

    同步练习册答案