
【题目】已知,抛物线y=ax+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
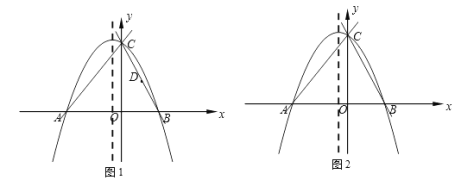
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线y=ax+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为![]() ;
;
(2)点G的坐标![]() 或
或![]()
(3)点F的坐标为![]() ,
, ![]() ,
,![]() ,
,![]()
【解析】
试题(1)将A(-3,0)和B(2,0)两点代入解析式,求出a、b的值,即可求得抛物线的解析式;(2))设点G的坐标为![]() ,过点D作DH⊥对称轴于点H,因点D是BC的中点,可得点D的坐标为
,过点D作DH⊥对称轴于点H,因点D是BC的中点,可得点D的坐标为![]() ,
,![]() ,由折叠的性质可得DH=DB,根据勾股定理可得
,由折叠的性质可得DH=DB,根据勾股定理可得![]() ,解得y的值,即可得点G的坐标;(3)分当BE为对角线和BE为菱形的边时两种情况讨论求解即可.
,解得y的值,即可得点G的坐标;(3)分当BE为对角线和BE为菱形的边时两种情况讨论求解即可.
试题解析:
(1)由题意得![]() ,
,
解得,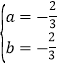
∴![]()
(2)设点G的坐标为![]()
过点D作DH⊥对称轴于点H
∵点D是BC的中点
∴点D的坐标为![]() ,
,![]()
由折叠得,DH=DB
∴![]()
∴![]()
∴点G的坐标为![]() 或
或![]()
(3)①当BE为对角线时,因为菱形的对角线互相垂直平分,所以此时D即为对称轴与AC的交点,F为点D关于x轴的对称点
设![]()
∵C![]() ,A
,A![]()
∴![]()
∴![]()
∴![]()
∴当![]() 时,
时,![]()
∴D![]()
∴F![]()
②当BE为菱形的边时,有DF∥BE
I)当点D在直线BC上时
易得![]()
设D![]() ,则点F
,则点F![]()
∵四边形BDFE是菱形
∴FD=DB
根据勾股定理得, ![]()
解得:![]() ,
,![]()
∴F![]() 或
或![]()
II)当点D在直线AC上时
设D![]() ,则点F
,则点F![]()
∵四边形BFDE是菱形
∴FD=FB
根据勾股定理得, ![]()
解得:![]() (舍去),
(舍去),![]()
∴F![]()
综上所述,点F的坐标分别为:![]() ,
, ![]() ,
,
![]() ,
,![]()


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
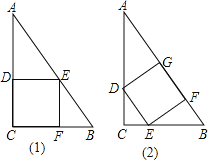
【题目】直角三角形的铁片ABC的两条直角边BC,AC的长分别为3cm和4cm,如图所示分别采用⑴,⑵两种方法,剪去一块正方形铁片,为了使剪去正方形铁片后剩下的边角料较少,试比较哪一种剪法较为合理,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (a ≠ 0)满足条件:(1)
(a ≠ 0)满足条件:(1)![]() ;(2)
;(2)![]() ;
;
(3)与x轴有两个交点,且两交点间的距离小于2.以下有四个结论:①![]() ;
;
②![]() ;③
;③![]() ;④
;④![]() ,其中所有正确结论的序号是
,其中所有正确结论的序号是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
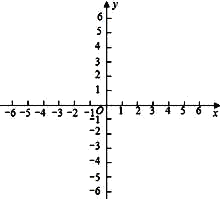
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A(-1,0),B(3,0)两点,与
轴交于A(-1,0),B(3,0)两点,与![]() 轴交于点C,顶点为D,下列结论正确的是( )
轴交于点C,顶点为D,下列结论正确的是( )

A. abc<0 B. 3a+c=0 C. 4a-2b+c<0 D. 方程ax2+bx+c=-2(a≠0)有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,O为坐标原点,点A(3,4),点B(6,0).
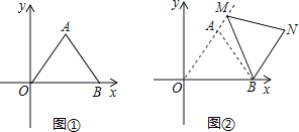
(1)如图①,求AB的长;
(2)如图2,把图①中的△ABO绕点B顺时针旋转,使O的对应点M恰好落在OA的延长线上,N是点A旋转后的对应点;
①求证:四边形AOBN是平行四边形;
②求点N的坐标.
(3)点C是OB的中点,点D为线段OA上的动点,在△ABO绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长方形镜面玻璃的四周,镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是3:1.已知镜面玻璃的价格是每平方米100元,边框的价格是每米20元,另外制作这面镜子还需加工费55元.如果制作这面镜子共花了210元,求这面镜子的长是__________![]() ,宽是___________
,宽是___________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
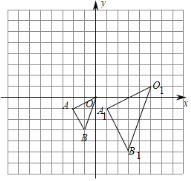
【题目】在如图所示的方格中,△OAB 的顶点坐标分别为 O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1 与△OAB 是以点 P 为位似中心的位似图形.
(1)位似中心 P 的坐标是 ,△O1A1B1与△OAB 的相似比为 ;
(2)以原点 O 为位似中心,在 y 轴的左侧画出△OAB 的另一个位似三角形![]() ,使它与△OAB 的相似比为 2:1,并写出点 B 的对应点
,使它与△OAB 的相似比为 2:1,并写出点 B 的对应点![]() 的坐标是 .
的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com