
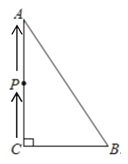
【题目】如图,△ABC中,![]() ,
,![]() ,
,![]() ,若点P从点C出发,以每秒1cm的速度沿折线C→A→B→C运动(回到C点后点P停止运动),设运动时间为t秒(
,若点P从点C出发,以每秒1cm的速度沿折线C→A→B→C运动(回到C点后点P停止运动),设运动时间为t秒(![]() ).
).
(1)若点P点AB边上,且满足![]() 时,求出此时t的值;
时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求出此时t的值;
(3)在运动过程中,当△BCP为等腰三角形时,直接写出所有满足条件的t的值.
【答案】(1)6.5s;(2)![]() s;(3)6.5s或6s或5.4s或3s.
s;(3)6.5s或6s或5.4s或3s.
【解析】
(1)根据题意,![]() ,
,![]() ,
,![]() ,可得AC=4cm,当P点在AB边上,且满足
,可得AC=4cm,当P点在AB边上,且满足![]() 时,则t=4+
时,则t=4+![]() 计算即可;
计算即可;
(2)当点P恰好在∠BAC的角平分线上时,做PD⊥AB于D,则PD=CP,利用三角形面积![]() ,代入数据计算即可得;
,代入数据计算即可得;
(3)当△BCP为等腰三角形时,分情况讨论:①当CP=BP时;②当CB=BP时;③当CP=CB时,分别计算即可.
(1)∵![]() ,
,![]() ,
,![]() ,
,
∴根据勾股数可知AC=4cm,
∵P点在AB边上,且满足![]() 时,
时,
∴PA=![]() AB=
AB=![]() cm,
cm,
又∵点P的速度是每秒1cm,
∴t=4+![]() =6.5(s);
=6.5(s);
故答案为:6.5s;
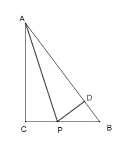
(2)过点P作PD⊥AB于D,如图所示,
∵点P恰好在∠BAC的角平分线上,
∴PD=PC,
又t=3+4+5-CP,
由![]() ,可得
,可得
![]() ×3×4=
×3×4=![]() ×4×CP+
×4×CP+![]() ×5×PD,
×5×PD,
∴CP=![]() ,
,
∴t=3+4+5-![]() =
=![]() (s),
(s),
故答案为:![]() s;
s;
(3)当△BCP为等腰三角形时,
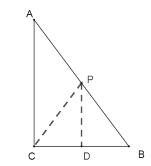
①当CP=BP时,点P在BC的垂直平分线上,作PD⊥BC于D,如下图所示:
∴点D是BC的中点,PD是△ABC的中位线,
∴点P是AB的中点,AP=BP=![]() AB=2.5cm,
AB=2.5cm,
∴t=6.5s;
②当CB=BP时,点P在AB上,如下图所示:
∴BP=CB=3cm,
∴t=4+5-3=6(s),
故答案为:6s;
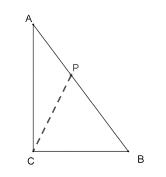
③CP=CB时,如下图所示:
点P在AB上,或者点![]() 在AC上两种情况,
在AC上两种情况,
若CP=CB时,过点C作CE⊥AB于E,
由等面积法求得CE=2.4cm,
在Rt△BEC中,由勾股定理得,
BE=1.8cm,BP=2BE=3.6cm,
∴t=4+5-3.6=5.4(s),
若C![]() =CB时,则t=C
=CB时,则t=C![]() =3s,
=3s,
故答案为:5.4s或3s;
综上所述,当△BCP为等腰三角形时,满足条件的t值为:6.5或6s或5.4s或3s;
故答案为:6.5s或6s或5.4s或3s.



 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ。若设运动时间为t(s)(0<t<2),解答下列问题:
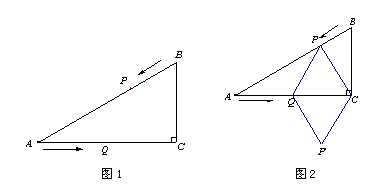
(1)当t为何值时?PQ//BC?
(2)设△APQ的面积为y(cm2),求y与t之间的函数关系?
(3)是否存在某一时刻t,使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由。
(4)如图2,连结PC,并把△PQC沿AC翻折,得到四边形PQP'C,那么是否存在某一时刻t,使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
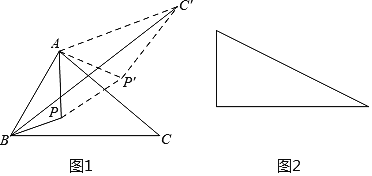
查看答案和解析>>
科目:初中数学 来源: 题型:
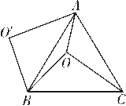
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;&
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AOBO′的面积为6+3![]() ;
;
⑤S△AOC+S△AOB=6+![]() .
.
其中正确的结论是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com