
【题目】甲同学从某小区出发步行前往学校.若干分钟后乙同学从学校出发骑自行车前往这个小区,他在小区停留一段时间后,以另一速度(千米![]() 分)沿原路返回.返回途中遇到了甲同学,用自行车搭载上甲同学减速返回学校,他们到达学校的时间比甲同学一直步行到学校的时间提前了
分)沿原路返回.返回途中遇到了甲同学,用自行车搭载上甲同学减速返回学校,他们到达学校的时间比甲同学一直步行到学校的时间提前了![]() 分钟.两人与学校的距离
分钟.两人与学校的距离![]() (千米)和乙同学从学校出发后所用的时间
(千米)和乙同学从学校出发后所用的时间![]() (分)之间的关系如图.
(分)之间的关系如图.
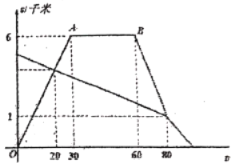
(1)两人第一次相遇时,距学校____________千米,![]() ____________(直接写出答案);
____________(直接写出答案);
(2)甲同学从小区出发多久后,乙同学从学校出发?
(3)求乙同学用自行车搭载上甲同学一起到学校的行进速度.
【答案】(1)4;0.25.(2)甲同学从小区出发20分钟后,乙同学从学校出发.(3)乙同学用自行车搭载上甲同学一起到学校的行进速度为0.1千米/分钟.
【解析】
(1)利用速度=路程÷时间可求出乙骑车前往该小区及乙骑车从该小区返回学校的速度,再由第一次相遇时距学校的距离(路程)=乙骑车前往该小区的速度×乙出发的时间,即可求出结论;
(2)由速度=路程÷时间可求出甲同学的速度,再由甲提前出发的时间=甲行走的路程÷甲的速度-乙出发的时间,即可求出结论;
(3)利用时间=路程÷速度可求出二者第二次相遇时甲同学继续按原速度走到学校所需时间,用其减去10可求出乙同学用自行车搭载上甲同学一起到学校所需时间,再利用速度=路程÷时间,即可求出乙同学用自行车搭载上甲同学一起到学校的行进速度.
解:(1)乙骑车前往该小区的速度为6÷30=0.2(千米/分钟),
乙骑车从该小区返回学校的速度为(6-1)÷(80-60)=0.25(千米/分钟),
两人第一次相遇时,距学校的距离为0.2×20=4(千米).
故答案为:4;0.25.
(2)甲同学的速度为(4-1)÷(80-20)=0.05(千米/分钟),
甲提前出发的时间为(6-4)÷0.05-20=20(分钟),
∴甲同学从小区出发20分钟后,乙同学从学校出发.
(3)二者第二次相遇时,若甲同学继续按原速度走到学校所需时间为1÷0.05=20(分钟),
∵20-10=10(分钟),
∴乙同学用自行车搭载上甲同学一起到学校的行进速度为1÷10=0.1(千米/分钟).
答:乙同学用自行车搭载上甲同学一起到学校的行进速度为0.1千米/分钟.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
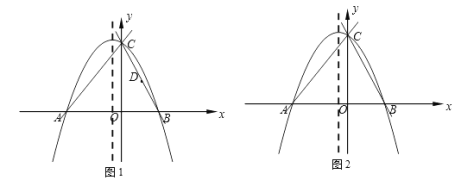
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线y=ax+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:
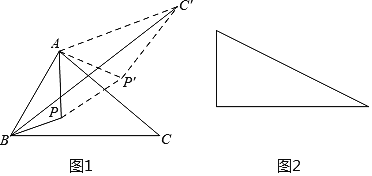
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
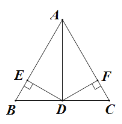
(1)求证:AB=AC;
(2)若∠BAC=60°,BC=6,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2140元,那么至少购买多少袋面粉?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com