
【题目】直线y=kx+3和x轴、y轴的交点分别为B、C,∠OBC=30°,点A的坐标是(![]() ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
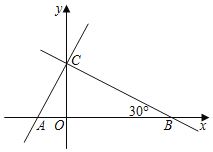
(1)求点B的坐标及k的值;
(2)求证:AC⊥BC;
(3)点M为直线BC上一点(与点B不重合),设点M的横坐标为x,△ABM的面积为S.
①求S与x的函数关系式;
②当S=6![]() 时,求点M的坐标.
时,求点M的坐标.
【答案】(1)B(3![]() ,0),k=﹣
,0),k=﹣![]() ;(2)见解析;(3)①S=
;(2)见解析;(3)①S=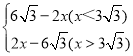 ;②点M的坐标为(0,3)或(6
;②点M的坐标为(0,3)或(6![]() ,-3).
,-3).
【解析】
(1)直线y=kx+3和y轴的交点为C,则点C(0,3),则BC=6,OB=3![]() ,则点B(3
,则点B(3![]() ,0),即可求解;
,0),即可求解;
(2)OA=![]() ,OC=3,则AC=2
,OC=3,则AC=2![]() ,则∠ACO=30°,即可求解;
,则∠ACO=30°,即可求解;
(3)①点M(x,-![]() x+3),S=
x+3),S=![]() ×AB×|yM|即可求解;
×AB×|yM|即可求解;
②将S=6代入①中的函数关系式,即可求解.
解:(1)直线y=kx+3和y轴的交点为C,则点C(0,3),
则BC=6,OB=3![]() ,
,
则点B(3![]() ,0),
,0),
将点B的坐标代入y=kx+3得:0=3![]() k+3,
k+3,
解得:k= -![]() ;
;
(2)在Rt△AOC中,OA=![]() ,OC=3,由勾股定理得AC=2
,OC=3,由勾股定理得AC=2![]() ,
,
∴∠ACO=30°,
∵∠OBC=30°,
∴∠BCO=60°,
∴∠ACB=∠ACO+∠BCO=90°,
∴AC⊥BC;
(3)①直线BC的表达式为:y=﹣![]() x+3,则点M(x,﹣
x+3,则点M(x,﹣![]() x+3),
x+3),
S=![]() ×AB×|yM|=
×AB×|yM|=![]() ×4
×4![]() ×|﹣
×|﹣![]() x+3|,即:S=
x+3|,即:S=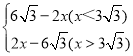 ;
;
②当S=6![]() 时,
时,
∵S=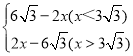
∴![]() 或
或![]()
解得:x=0或x=6![]() ,
,
故点M的坐标为(0,3)或(6![]() ,-3).
,-3).


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
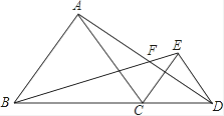
【题目】如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求残片所在圆的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
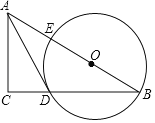
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com